Векторный способ задания движения точки. Координатный способ задания движения точки, страница 12

а		б
Рис. 4.17

Решение. Вычислим угловые скорости звеньев  -  и  - :

,   ;

,  ,

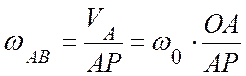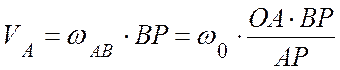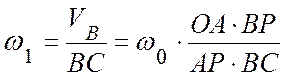Здесь точка Р - точка мгновенного центра скоростей шатуна АВ. Его положение определяется точкой пересечения перпендикуляром к векторам скоростей точек А и В (рис. 4.17, б).

Из  определяем расстояния составляют:  см;  см; тогда

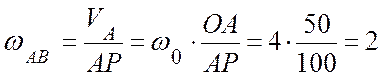 (с^-1);

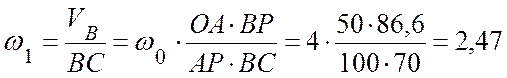 (с^-1).

Аналитический способ

Применим теорему об ускорениях при плоском движении тела к точке В. За полюс выбираем  точку А, ускорение в этой точке известно:

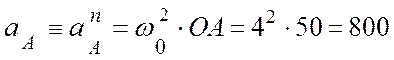 (см/с²);

Тогд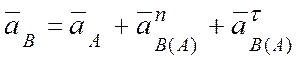а                      ,                                                       (а)

здесь 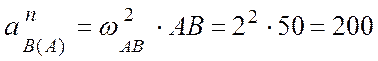  (см/с²);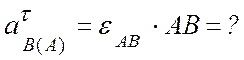

В полученном векторном равенстве (а) три неизвестных: модуль и направление ускорения в точке В -  и угловое ускорение шатуна АВ -  ().

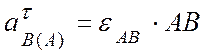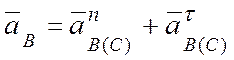Для решения задачи необходимо записать еще одно уравнение. За второй полюс выберем точку , , тогда (рис. 4.17 б):

,                                               (б)

здесь 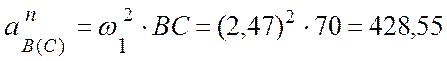  (см/с²);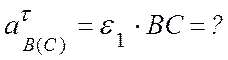

В полученном векторном равенстве (б) тоже три неизвестных: модуль и направление ускорения в точке В -  и угловое ускорение кривошипа  - . ().

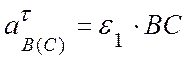Получили систему уравнений:

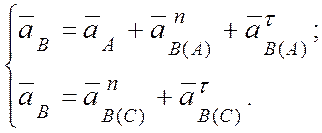                                             (в)

Исключим вектор  из (в). Для этого приравняем правые части уравнений (в) между собой, получим следующее векторное уравнение, которое будет содержать только две неизвестные величины:  и :

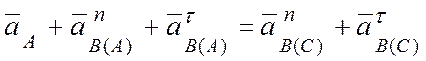.                                        (г)

Совместим с точкой В начало декартовой системы координат (рис. 4.18, а), и спроецируем равенство (г) на эти оси:

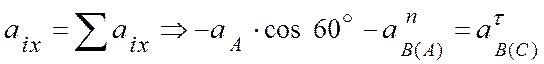;                      (1)

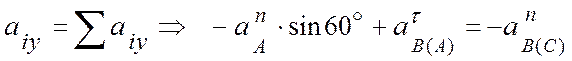.                   (2)

Получили систему двух скалярных уравнений с двумя неизвестным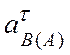и:  и 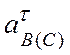. Решая последовательно уравнения (1-2), получаем:

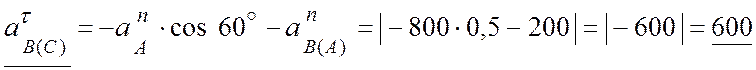          (см/с²);

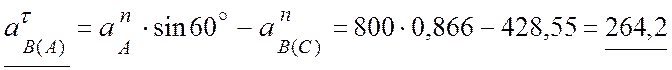 (см/с²).

а		б
Рис. 4.18

Знак (-) модуля 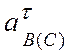 показывает, что истинное направление этого вектора противоположно выбранному на схеме (рис. 4.18 б).

Вычислим ускорение точки В:

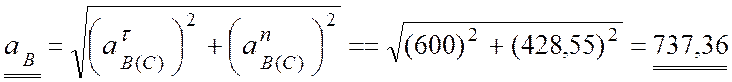 (см/с²).

Направление вектора  получаем построением параллелограмма на векторах 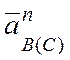 и 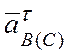 (рис. 4.18, б).

Графический (геометрический) способ

Ускорение шарнира В получим построением многоугольника ускорений (рис. 4.19). Рассмотрим векторное равенство (г):

,  

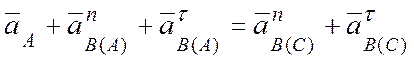здесь

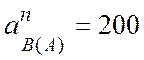 (см/с²),    (см/с²),  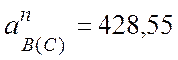  (см/с²).

В выбранном масштабе откладываем из точки В, параллельно ОА, ускорение . Из конца этого вектора в том же масштабе, параллельно оси звена АВ, откладываем нормальную составляющую ускорения 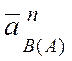, и из его конца проводим пунктирную прямую I-I, перпендикулярную 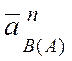 (параллельную неизвестному ускорению 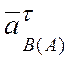). Затем из точки В, в том же масштабе, откладываем нормальную составляющую ускорения 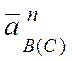 - вдоль звена ВС, из конца этого вектора проводим перпендикулярную ему пунктирную прямую II-II, параллельную неизвестному ускорению 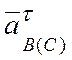 (рис. 4.19).

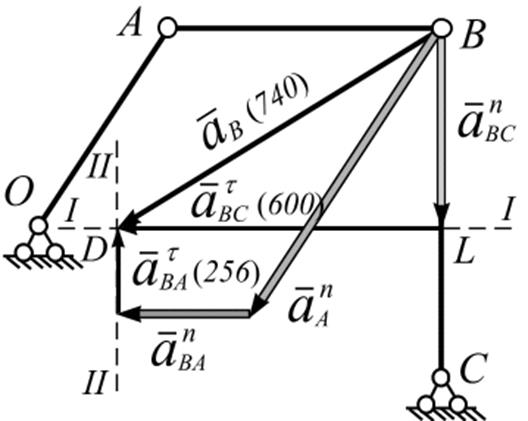
Рис. 4.19

Обозначим точку пересечения прямых I-I и II-II буквой D. Соединим точку В и точку D, полученная прямая  соответствует ускорению точки В - ; прямая  соответствует ускорению 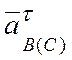; прямая  соответствует ускорению 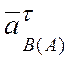. Замеряем длину отрезков, с учетом принятого масштаба, получаем:

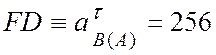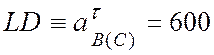 (см/с²);    (см/с²);    см/с²).

Результаты получены двумя разными способами, хорошо согласуются друг с другом.

Ответ: (см/с²).

(!!! Алгоритм решения

При решении задач на вычисление уравнений движения плоского твердого тела и вычисление скоростей точек, жестко связанных с плоской фигурой, рекомендуется такая последовательность действий:

·  выбираем неподвижную систему координат и точку С (полюс), жестко связанную с плоской фигурой;

·  составляем уравнения движения плоской фигуры: определяем координаты полюса относительно неподвижной системы координат , ; проводим через точку C прямую, определяем угол , который эта прямая составляет с горизонтальной неподвижной осью;

·  вычисляем скорость полюса  и скорость любой точки тела (например, точки В), как точки, мгновенно вращающейся вокруг полюса - ;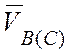

·  вычисляем скорость любой точки, жестко связанной с телом, (движущейся вместе с полюсом и вращающейся вокруг полюса), по теореме о скоростях точек тела при его плоскопараллельном движении: .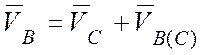

Если определить  аналитически сложно, находим мгновенный центр скоростей для заданного положения твердого тела, восставляя перпендикуляры к векторам скоростей двух точек плоской фигуры (точки В и С, направление вектора скорости в точках С и В известно), и определяем мгновенную угловую скорость фигуры.