Векторный способ задания движения точки. Координатный способ задания движения точки, страница 5

2. Простые механизмы

J

Вспомни теорию

Вращением твердого тела вокруг неподвижной оси называется такое его движение, при котором точки тела, расположенные на прямой, остаются неподвижными в течение всего времени движения. Эта прямая называется осью вращения.

 – уравнение вращения твердого тела вокруг неподвижной оси;

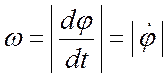 – угловая скорость тела;

 – угловое ускорение тела.

Рис. 2.1	Рис. 2.2

Если знаки производных одинаковые (, , , ), тело вращается ускоренно (против или по движению часовой стрелки, соответственно). Если знаки производных разные, например , , – тело вращается замедленно. Угловую скорость и угловое ускорение на рисунках изображают дуговыми стрелками вокруг оси вращения тела, рис. 2.2.

Скорости и ускорения точек твердого тела. Скорость точки тела при его вращении вокруг неподвижной оси пропорциональна кратчайшему расстоянию от точки до оси вращения:

.

Скорость точки направлена по касательной к траектории и, следовательно, перпендикулярна прямой, соединяющей точку с центром вращения (рис. 2.2).

Ускорение точки М разлагаем на касательную и нормальную составляющие (рис. 2.2):

, ,  , .

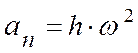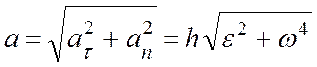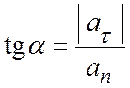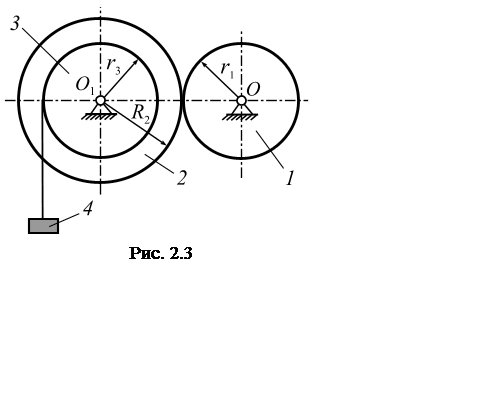
Задача 2.1. Диск 1 вращается вокруг неподвижной оси, уравнение вращения диска задано: 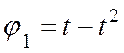 (рад) (рис. 2.3). Диск 1 приводит во вращение диски 2, 3, имеющие общую неподвижную ось вращения и жестко скрепленные друг с другом. Диски 1, 2 связаны зубчатой передачей. На диск 3 намотана нерастяжимая нить, на конец которой привязан груз 4. Вычислить ускорение точки А (лежит на ободе диска 2) и скорость груза 4 в момент времени  с, если  м,  м,  м.

Решение. Вычислим угловую скорость и угловое ускорение диска 1 в момент времени  с:

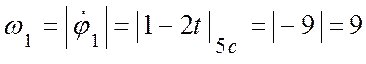 (с^-1);

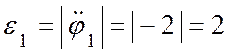 (с^-2).

а	б
Рис. 2.4

Получили:  и , следовательно, дуговые стрелки для  и  следует направить в сторону часовой стрелки (рис. 2.4, а). Тогда диски 2, 3 будут вращаться против часовой стрелки за счет зубчатой передачи, а груз 4 опускаться.

Запишем уравнения связи.

Справка Длина дуги, угол поворота и радиус связаны соотношением   .

1. Перемещения  точек соприкосновения 1-го и 2-го диска при отсутствии скольжения между ними одинаковые, поэтому

,   откуда   .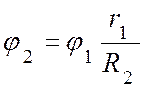

Дифференцируя правую и левую части, получим

,   .

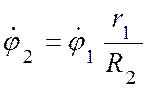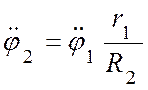Откуда: 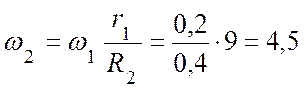   (с^-1),    (с^-2).

Вычислим ускорение в точке А (рис. 2.4, б):

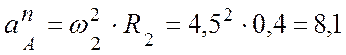 (м/с²); 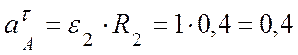   (м/с²);

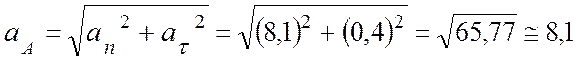(м/с²).

2. Перемещения точек соприкосновения груза 4 (через нерастяжимую нить) и диска 3 одинаковые, поэтому

.

Дифференцируя правую и левую части, получим

 м/с; здесь 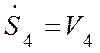 - скорость тела 4.

Ответ:  ускорение   (м/с²);  скорость   (м/с).

Задача 2.2. Механизм (рис. 2.5) состоит из двух ступенчатых дисков (2 и 3), связанных ременной передачей, барабана 4, соединенного с диском 3 нерастяжимым тросом, и груза 1, привязанного к концу нити, намотанной на диск 2. Уравнение движения ступенчатого диска 3: 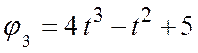 (рад). Радиусы ступеней дисков составляют соответственно  м,  м;  м;  м; радиус барабана  м.

В момент времени  с вычислить:

- скорости точек А, В, С и D, расположенных на ободе дисков, скорость точки Е, расположенной на ободе барабана;

- ускорения груза 1 и точек С, Е.

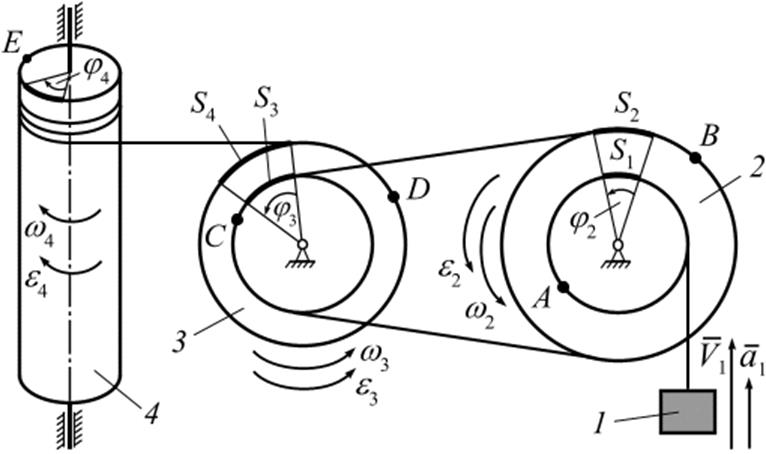
Рис. 2.5

Решение.

1.  Определим направление движения звеньев механизма. Вычислим угловую скорость и угловое ускорение ведущего диска 3 для заданного момента времени  с:

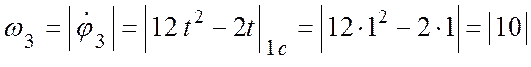 (с^-1);

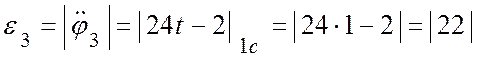 (с^-2).

Движение ведущего диска 3 ускоренное и направлено против часовой стрелки, т.к. , . Следовательно, движение всех звеньев механизма будет ускоренным, как показано дуговыми стрелками на рис. 2.5.

2.  Запишем уравнения связей для заданного механизма.

Ведущим звеном системы является ступенчатый диск 3.

2.1.  Диски 3 и 2 соединены нерастяжимым ремнем:

,   откуда   ,

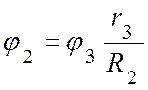тогда 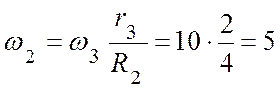   (с^-1),  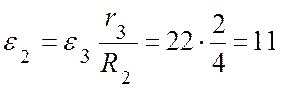  (с^-2).

2.2.  Диск 3 и барабан 4 соединены нерастяжимым тросом:

,   откуда   ,

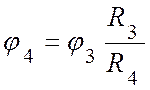тогда 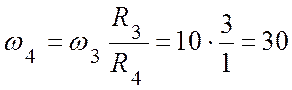   (с^-1);  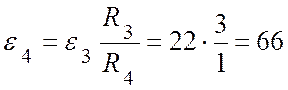  (с^-2).

2.3.  Диск 2 и груз 1 соединены нерастяжимой нитью:

,   откуда    (м/с),

 (м/с²).

3.  Вычислим скорости точек.

Точки С и D находятся на ободе диска 3:

 (м/с);    (м/с).

Точки А и В находятся на ободе диска 2:

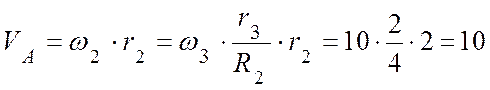 (м/с);

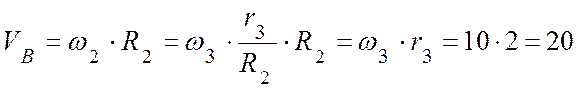 (м/с).

Точка Е находится на ободе барабана 4:

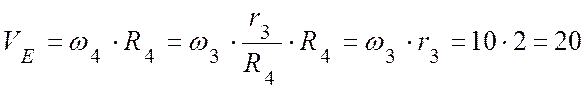 (м/с).

Векторы скоростей точек строятся перпендикулярно соответствующим радиусам дисков и барабана в направлении их угловых скоростей (рис. 2.6).

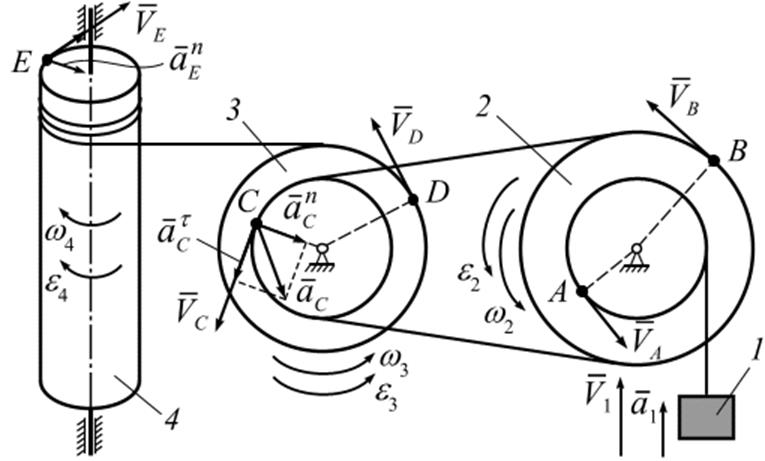
Рис. 2.6

Скорость груза 1:

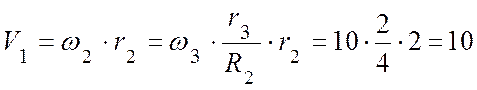 (м/с).

4.  Вычислим ускорения точек С, Е.

Точка С находится на ободе диска 3, с учетом его вращательного движения ускорение этой точки:

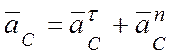,   где 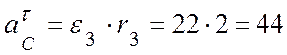   (м/с²),

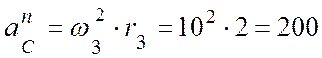 (м/с²);

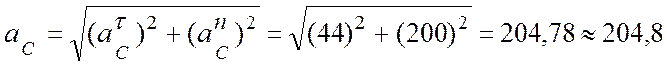 (м/с²).

Точка Е находится на ободе барабана 4, который совершает вращательное движение. Тогда, аналогично точке С, ускорение точки Е:

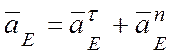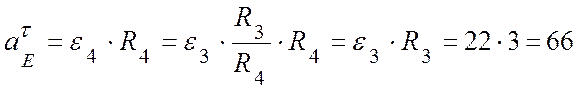,    (м/с²),

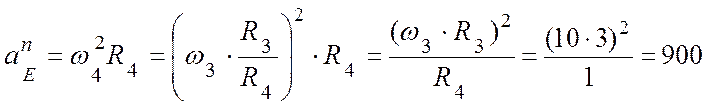 (м/с²);

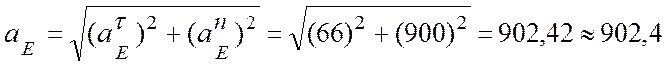 (м/с²).

5.  Вычислим ускорение груза 1.

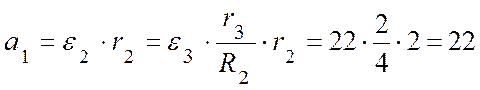 (м/с²).

Ответ:   (м/с),   (м/с),  (м/с),  (м/с),

 (м/с);   (м/с²),   (м/с²),  (м/с²).

(!!! Алгоритм решения

Первый тип задач (прямая задача) - задано уравнение вращения твердого тела , требуется вычислить угловую скорость, угловое ускорение, скорость и ускорение точек твердого тела:

·  выбираем систему координат так, чтобы одна из осей (для определенности ось z) совпадала с осью вращения;

·  составляем уравнение вращения твердого тела, т.е. зависимость , если она не задана явно;

·  вычисляем первую производную по времени от , вычисляем угловую скорость вращения тела ;

·  вычисляем вторую производную по времени от , находим угловое ускорение вращения тела ;

·  связываем с исследуемой точкой систему координат ; вычисляем модуль скорости, касательную  и нормальную , составляющие ускорение точки, принадлежащей вращающемуся телу;

·  вычисляем полное ускорение точки по модулю и направлению.

Второй тип задач (обратная задача) - задано угловое ускорение  или угловая скорость твердого тела ; требуется вычислить уравнение вращения , скорость любой точки твердого тела , ускорение любой точки твердого тела :

·  формулируем начальные условия задачи;