Векторный способ задания движения точки. Координатный способ задания движения точки, страница 8

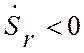Векторы  и  направлены в одну сторону по , т.к.  и 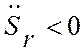, следовательно, относительное движение точки ускоренное (рис. 3.5, б). Вектор  направлен по оси .

3.2. Переносное ускорение точки М.

Угловое ускорение пластины:

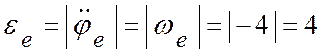 (с^-2)

т.к. , , вращение диска – равнозамедленное, дуговые стрелки  и  направлены в разные стороны (рис. 3.5, а).

Вектор переносного ускорения:

,

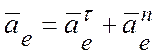где 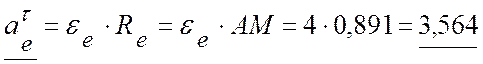   (м/с²);

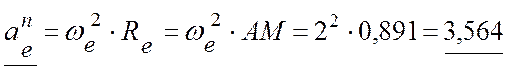 (м/с²).

Вектор  направлен по , вектор  - по  (рис. 3.5, а).

3.3. Ускорение Кориолиса:

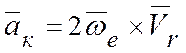,   или   ,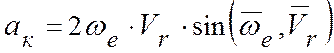

т.к. соприкасающиеся плоскости переносного и относительного движений совпадают, вектор  перпендикулярен  плоскости вращения, имеем:

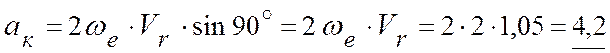 (м/с²).

Направление ускорения Кориолиса  определяем по правилу Жуковского: вектор  поворачиваем на  по направлению дуговой стрелки  (рис. 3.5, б).

3.4. Абсолютное ускорение точки М:

,

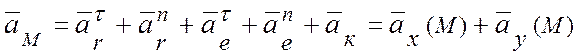здесь

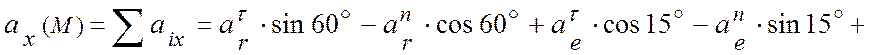
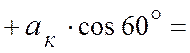
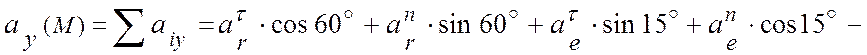
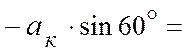
 (см/с²);

 (см/с²);

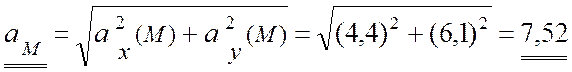 (м/с²).

Направление абсолютного ускорения:

.

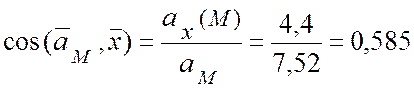Ответ:    (м/с);    (м/с²).

Задача 3.3.Фигурная пластина вращается по заданному уравнению  (рад) относительно неподвижной горизонтальной оси. По диагонали пластины из точки О движется точка М согласно заданному уравнению 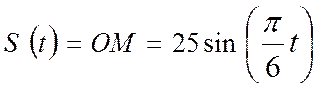 (см). Размеры пластины  см,  см (рис. 3.6).

Рис. 3.6

В момент времени  с для точки М требуется:

1)  Вычислить абсолютную скорость, показать геометрически направление векторов относительной, переносной и абсолютной скорости.

2)  Вычислить абсолютное ускорение, показать геометрически направление векторов относительного, переносного ускорения и ускорения Кориолиса.

Решение.

1.  Вычислим абсолютную скорость точки М.

Абсолютная скорость точки при ее сложном движении складывается из векторов относительной и переносной скорости:

.

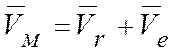1.1. Относительным является движение точки М по диагонали прямоугольной пластины, оно задано уравнением 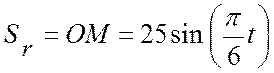. Определим положение точки М на диагонали пластины:

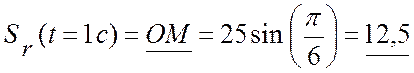 см.

Относительная скорость точки:   ;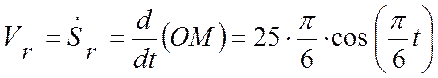

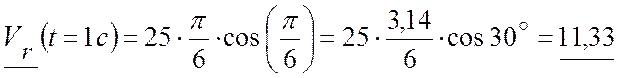 (см/с).

Относительное движение точки М прямолинейное вверх (рис. 3.7, а), вектор  направлен вдоль диагонали пластины по ходу относительного движения, т.к. .

а		б
Рис. 3.7
Справка. Из геометрии пластины:  (см);    (см);  (см).;  (см).

Переносное движение точки М криволинейное, т.к. пластина вращается относительно оси , по окружности радиусом  (рис. 3.7,б).

Параметры переносного движения:

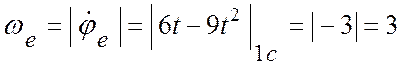 (с^-1); 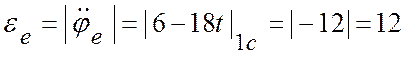 (с^-2).

Знак  определяет направление вращения пластины по часовой стрелке, и вектор скорости  строится в указанном направлении переносного вращения (рис. 3.7,б). Модуль переносной скорости:

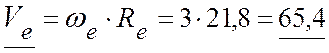 (см/с);

Плоскости относительного и переносного движений в данной задаче взаимно перпендикулярны, следовательно . Тогда модуль абсолютной скорости точки М рассчитывается так:

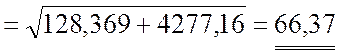 (см/с).

2.  Рассчитываем абсолютное ускорение точки М.

Абсолютное ускорение точки при ее сложном движении геометрически складывается из относительного, переносного ускорения и ускорения Кориолиса:

.

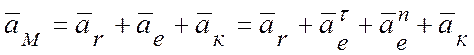2.1. Относительное ускорение:

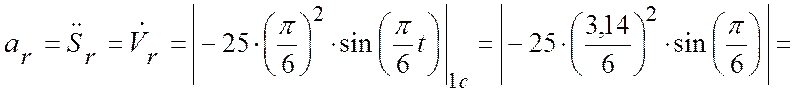
 (см/с²).

Векторы  и  направлены вдоль диагонали пластины в противоположные стороны, т.к. , ; следовательно, относительное движение точки замедленное (рис. 3.7, а).

2.2. Переносное ускорение

Угловое ускорение пластины (переносное угловое ускорение точки)

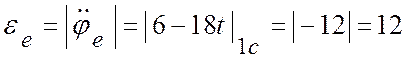 (с^-2),

т.к. , переносное вращение относительно оси  ускоренное по часовой стрелке (рис. 3.7, б).

Модули векторов переносного ускорения точки М (рис. 3.7, б):

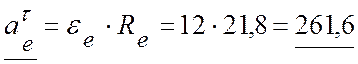 (см/с²); 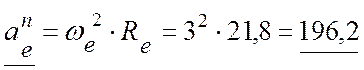 (см/с²).

2.3. Ускорение Кориолиса

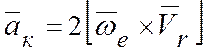,   или   ,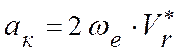

где 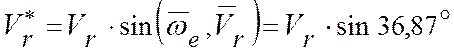               (рис. 3.7, б);

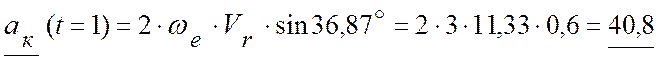 (см/с²).

Вектор ускорения Кориолиса  получаем поворотом вектора  на  в направлении , т.е. по часовой стрелке, в соприкасающейся плоскости переносного движения  (рис. 3.7, б).

Строим векторы переносного ускорения и ускорения Кориолиса в соприкасающейся плоскости переносного движения - плоскости .

Плоскости относительного и переносного движений взаимно перпендикулярны, тогда абсолютное ускорение точки М рассчитывается по формуле

.

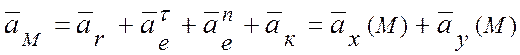С учетом расположения векторов, входящих в теорему, в двух соприкасающихся плоскостях    ,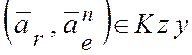     

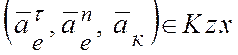
(рис. 3.7, а, б), расписываем проекции векторов на указанные оси:

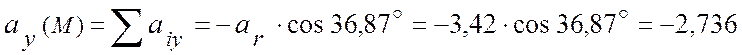 (см/с²);

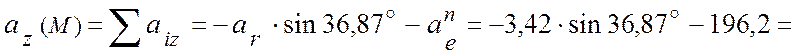
 (см/с²);

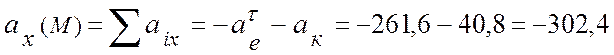 (см/с²);

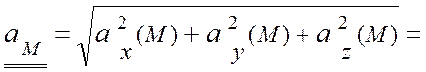
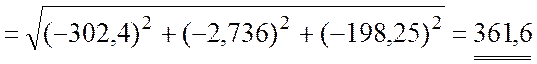 (см/с²).

Ответ:    (см/с);    (см/с²).

(!!! Алгоритм решения

Заданы уравнения относительного  и переносного движения ; требуется вычислить скорость абсолютного движения:

·  раскладываем абсолютное движение точки на два составных движения - переносное и относительное;

·  выбираем две системы координат: абсолютную, условно принимаемую неподвижной, и относительную, которую связываем с движущимся телом;

·  составляем уравнения относительного движения точки и уравнения переносного движения точки;

·  мысленно остановив переносное движение, вычисляем скорость  и ускорение точки  в относительном движении;

·  мысленно остановив относительное движение, вычисляем угловую скорость переносного движения  и угловое ускорение точки в переносном движении ;

·  по известным угловой скорости переносного движения  и скорости  в относительном движении, используя правило Жуковского, вычисляем ускорение Кориолиса точки ;

·  пользуясь методом проекций, вычисляем проекции абсолютной скорости и абсолютного ускорения точки на оси координат;

·  по вычисленным проекциям абсолютной скорости и абсолютного ускорения находим искомую абсолютную скорость и  абсолютное ускорение по модулю и направлению.