Векторный способ задания движения точки. Координатный способ задания движения точки, страница 10

Тогда, каждая точка тела будет мгновенно двигаться по окружности, радиус которой определяется расстоянием этой точки до МЦС (рис. 4.4), дуга, по которой пройдет каждая точка тела в единицу времени, будет равна  где  - расстояние точки до МЦС, т.е.

Рис.4.4

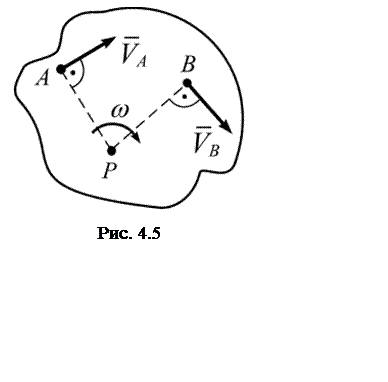
Если положение МЦС известно, то, приняв МЦС за полюс (), любые точки, например точки А и В (рис. 4.5), будут направлены перпендикулярно радиусу, равному расстоянию от этой точки до точки МЦС:

;

Здесь АР и ВР – расстояние от точек А и В до МЦС, т.е. до точки Р.

Следовательно, если положение МЦС известно, то скорости точек тела вычисляют так же, как и в случае вращения тела в плоскости вокруг неподвижного центра

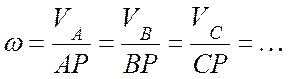
Частные случаи вычисления точки МЦС.

o  Цилиндрическое тело катится по неподвижной поверхности, точка касания Р является МЦС (рис. 4.6, а), т.е. тело мгновенно вращается относительно точки касания Р.

o  Скорости точек А и В тела параллельны друг другу, причем линия АВ не перпендикулярна к  и  (рис. 4.6 б), точка МЦС находится в бесконечности, тогда 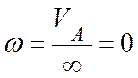, т.е. тело движется мгновенно-поступательно.

o  Скорости точек А и В тела параллельны друг другу и при этом , положение точки МЦС определяется построениями, показанными на рис. 4.6 в, г; тело совершает мгновенно-вращательное движение вокруг точки Р.

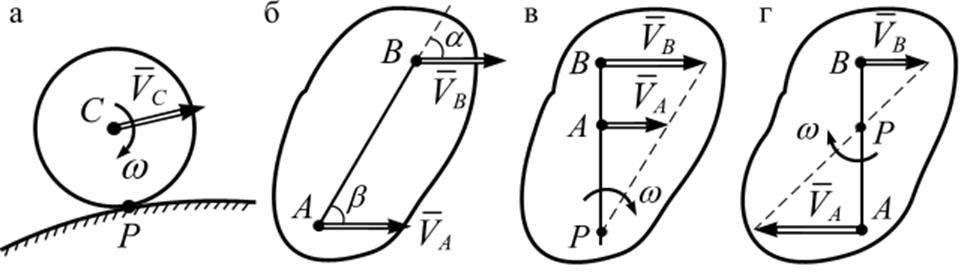
Рис. 4.6

Задача 4.2. Кривошипно-шатунный механизм (рис. 4.7) состоит из кривошипа ОА, шатуна АВ и ползуна В. Кривошип ОА длиной  м вращается с угловой скоростью  с^-1. Длина шатуна  м. При заданном угле  вычислить:

1.  угловую скорость шатуна АВ – ;

2.  скорость ползуна В;

3.  рассмотреть положение механизма, когда  и .

а		б
Рис. 4.7

Решение. Вычислим модуль скорости точки А кривошипа:

 (м/с).

Направлена скорость перпендикулярно ОА в сторону вращения кривошипа (рис. 4.7, а).

Вектор скорости ползуна  направлен вдоль дорожек. Восстановим перпендикуляры к векторам  и . Точка МЦС (точка Р) лежит на их пересечении. Из геометрии задачи вычислим АР и ВР (рис. 4.7, б).

Имеем:

из   м;  м;

из

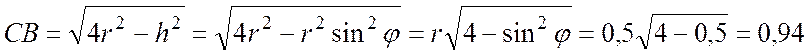 м;

 м;

 м;    м.

Напомним, что угол . Тогда

;   ;   .

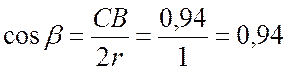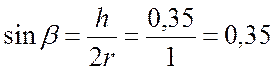Угловая скорость шатуна АВ:

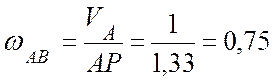 (с^-1).

Если механизм нарисован в масштабе, то АР и ВР измеряются линейкой.

2. Скорость ползуна (скорость в точке В):

 (м/с).

Проверим правильность полученных результатов, используя основную теорему кинематики. Имеем (рис. 4.6, б):

угол САВ=,

тогда, согласно основной теореме кинематики, имеем:

3. Угол  (рис. 4.7, а).

Восстановим перпендикуляры к векторам  и . Точка МЦС (точка Р) лежит на их пересечении и совпадает с точкой В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей, тогда . В этом положении шатун АВ совершает мгновенное вращение вокруг точки В с угловой скоростью

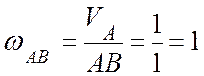 (с^-1).

Распределение скоростей шатуна показано на рис. 4.8 а.

Угол  (рис. 4.8, б).

а		б
Рис. 4.8

Скорости  и  направлены параллельно друг другу, и перпендикуляры к ним пересекаются в бесконечности, тогда 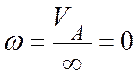. Следовательно, в этом положении шатун совершает мгновенно-поступательное движение, и все точки шатуна АВ имеют одинаковую скорость, равную  (м/с).

Ответ:    (с^-1);    (м/с).

J

Вспомни теорию

4.3. Ускорение при плоском движении твердого тела

Ускорение какой-либо точки тела при его плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении тела вокруг полюса:

.

Здесь: 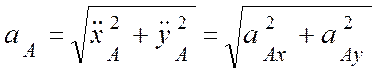   – ускорение полюса;

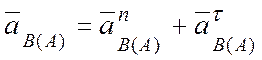 – ускорение точки В при ее вращении вместе с телом вокруг полюса А:

нормальная составляющая ускорения направлена по нормали, т.е. по АВ к полюсу А, и равна ;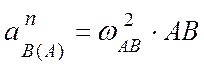

касательная составляющая ускорения направлена ^ АВ в сторону дуговой стрелки  и равна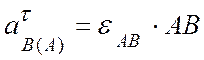

Задача 4.3.Кривошип ОА длиной 60 см вращается ускоренно относительно оси О и приводит в движение ролик 1 радиусом  см, который катится без скольжения по неподвижному колесу 2 (рис. 4.9). Параметры вращения кривошипа в данный момент времени  с^-1,  с^-2. Вычислить угловую скорость  и угловое ускорение  ролика, вычислить скорость и ускорение точки В, находящейся на ролике на расстоянии 10 см от точки А.

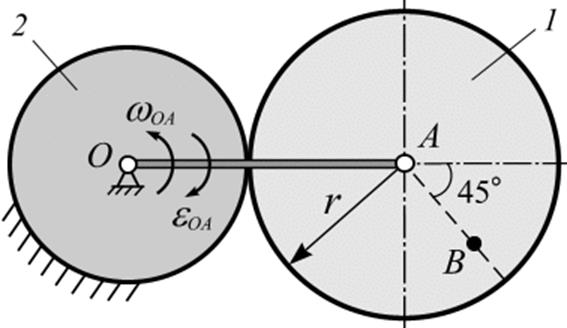
Рис. 4.9

Решение. Кривошип ОА совершает вращательное движение относительно оси, проходящей через неподвижный центр О. Скорость и ускорение точки А кривошипа вычисляют по формулам:

 (см/с);

.

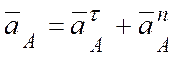Подвижный ролик движется плоскопараллельно. Вычислим  и подвижного ролика. Плоское движение ролика можно привести к мгновенно-вращательному движению относительно мгновенного центра скоростей (МЦС), этим центром является точка касания Р (рис. 4.10).

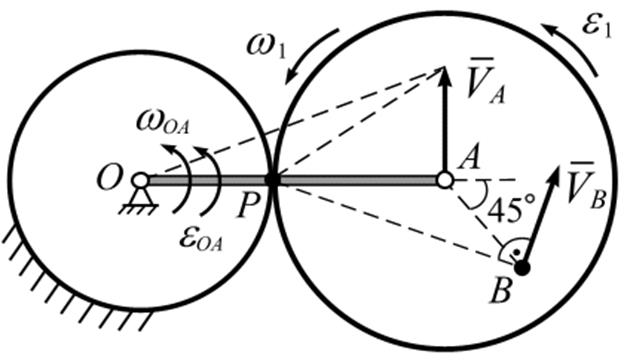
Рис. 4.10

Запишем уравнение связи между движениями кривошипа и ролика. Точка А одновременно принадлежит кривошипу ОА и ролику 1. Следовательно, перемещение точки А:

,   т.е.   .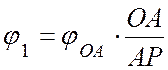

Угловая скорость и угловое ускорение ролика 1 тогда вычисляются:

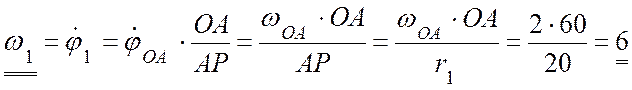 (с^-1);

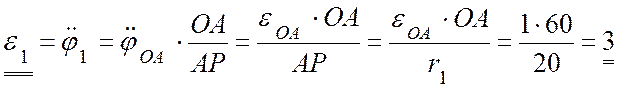 (с^-2).

Угол вращения ролика относительно точки Р(точка МЦС), совпадает с углом вращения кривошипа (рис. 4.9). Направления вращения  и  ролика 1 совпадают, отмечаем их дуговыми стрелками; следовательно, движение ролика 1 является ускоренным, как и кривошипа ОА.

Скорость точки В.

Точка В находится на ролике 1, следовательно, её скорость определяется как скорость точки, вращающейся вокруг МЦС, т.е.точки Р:

.

Из геометрии задачи определим по теореме косинусов расстояние ВР:

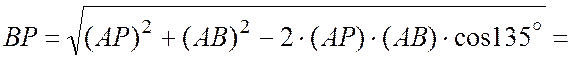
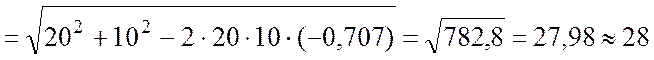 (см).

Тогда скорость точки В:

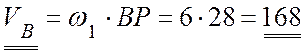 (см/с).

Вектор  перпендикулярен отрезку ВР и направлен в сторону вращения  ролика (рис. 4.10).

3.  Ускорение точки В.

Ускорение точки В складывается из ускорения полюса и ускорения точки В при её вращении вместе с роликом вокруг этого полюса. За полюс примем точку А, т.к. её ускорение известно.

Тогда ускорение точки В запишется (рис. 4.11):

.

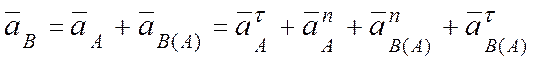а		б
Рис. 4.11

Здесь:

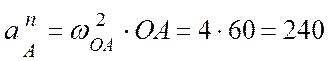 (см/с²) - нормальная составляющая ускорения полюса, направлена от точки А к центру О;