1. Точка В. Точка движется прямолинейно вдоль
оси ![]() . Следовательно, в любой момент
времени координата
. Следовательно, в любой момент
времени координата ![]() , и движение этой точки
будет определяться только координатой
, и движение этой точки
будет определяться только координатой ![]() (рис.
1.9).
(рис.
1.9).
Имеем:
![]() ,
тогда координата
,
тогда координата ![]() .
.
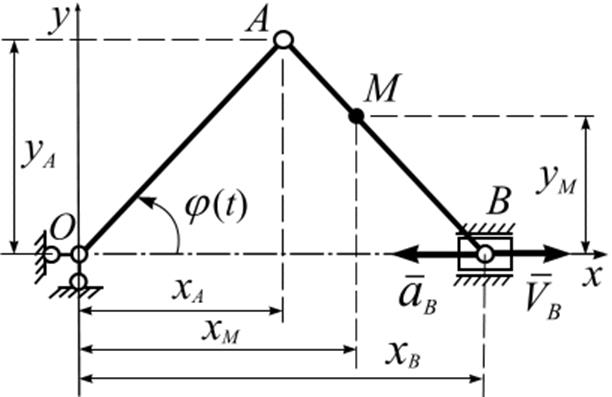
Рис. 1.9
Скорость точки В:
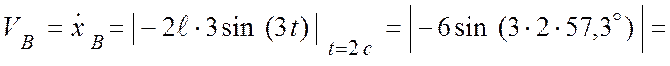
![]() см/с;
см/с;
|
Справка:
|
Ускорение точки В:
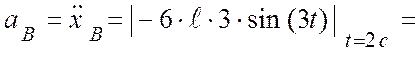
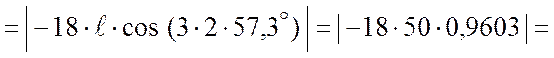
![]() см/с2.
см/с2.
Знаки производных: ![]() ,
, ![]() , следовательно, точка В
движется замедленно (рис. 1.9).
, следовательно, точка В
движется замедленно (рис. 1.9).
2. Точка М. Координаты точки М (рис. 1.9):
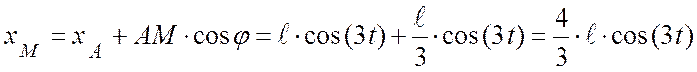 ;
;
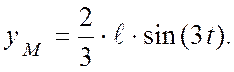
Скорость точки М для ![]() с:
с:
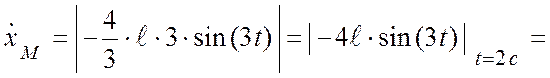
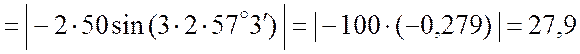 (см/c);
(см/c);
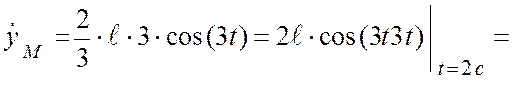
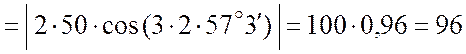 (см/c);
(см/c);
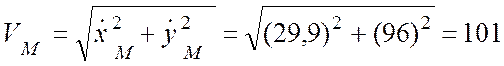 (см/c).
(см/c).
Ускорение точки М
для ![]() с:
с:

![]() (см/c2);
(см/c2);

![]() (см/c2);
(см/c2);
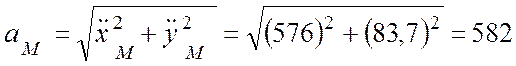 (см/c2).
(см/c2).
Знаки ![]() ,
, ![]() ,
следовательно, точка М вдоль оси
,
следовательно, точка М вдоль оси ![]() движется
замедленно;
движется
замедленно; ![]() ,
, ![]() ,
следовательно, точка М вдоль оси
,
следовательно, точка М вдоль оси ![]() движется
ускоренно.
движется
ускоренно.
Ответ: ![]() см/c;
см/c;
![]() см/c2;
см/c2; ![]() см/c;
см/c;
![]() см/c2.
см/c2.
Задача 1.4. Точка движется в плоскости ![]() .
Уравнение движения точки задано координатным способом:
.
Уравнение движения точки задано координатным способом:
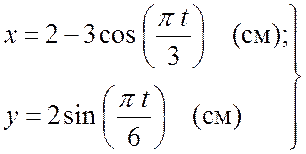 , где
, где ![]() и
и ![]() выражены
в см,
выражены
в см, ![]() - в с. (а)
- в с. (а)
Требуется:
1. Построить траекторию движения точки в декартовой системе координат.
2. Вычислить положение точки в начальный момент времени ![]() , направление движения точки по
траектории и положение точки на траектории при
, направление движения точки по
траектории и положение точки на траектории при ![]() с.
с.
3. Вычислить вектор скорости ![]() .
.
4. Вычислить вектор ускорения ![]() точки
при
точки
при ![]() с.
с.
Решение. 1. Построим траекторию движения точки. Для этого
в декартовой системе координат определим область, в которой движется точка,
т.е. область значений ![]() и
и ![]() .
Функции
.
Функции ![]() и
и ![]() - ограничены, т.е.
- ограничены, т.е. ![]() ,
, ![]() , получаем (см. рис. 1.10):
, получаем (см. рис. 1.10):
![]() ;
; ![]() .
.
![]() , если
, если 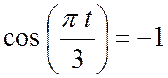 ,
тогда
,
тогда 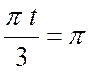 ,
, ![]()
![]() , если
, если 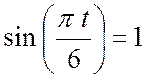 ,
тогда
,
тогда 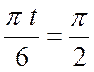 ,
, ![]()
Получим зависимость ![]() .
Для этого из уравнений (а) исключим параметр
.
Для этого из уравнений (а) исключим параметр ![]() .
Введём обозначение
.
Введём обозначение 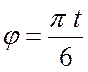 , тогда уравнения (а)
перепишутся в виде
, тогда уравнения (а)
перепишутся в виде
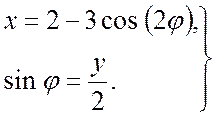 (б)
(б)
Распишем первое уравнение системы (б), используя
формулу двойного угла (![]() ), приведем
подобные члены и выразим
), приведем
подобные члены и выразим ![]() через
через ![]() :
:
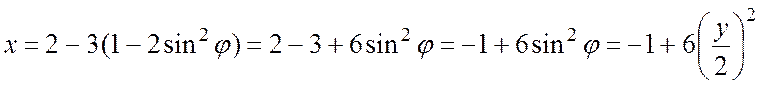 ,
,
или
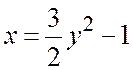 . (с)
. (с)
Анализируем траекторию движения точки.
Траекторией точки является парабола с координатой вершины (-1, 0); ветви
параболы вытянуты вдоль оси ![]() (рис. 1.10).
(рис. 1.10).
При ![]() функции
функции ![]() и
и ![]() возрастают
(рис. 1.10), поэтому точка М из положения
возрастают
(рис. 1.10), поэтому точка М из положения ![]() начинает
движение по верхней ветви параболы до положения
начинает
движение по верхней ветви параболы до положения ![]() ;
далее точка движется обратно по верхней ветви траектории, через точку с координатами
;
далее точка движется обратно по верхней ветви траектории, через точку с координатами
![]() продолжает движение по нижней ветви
параболы до положения
продолжает движение по нижней ветви
параболы до положения ![]() , далее движется
обратно и т.д. Точка совершает колебательные движения по параболе.
, далее движется
обратно и т.д. Точка совершает колебательные движения по параболе.
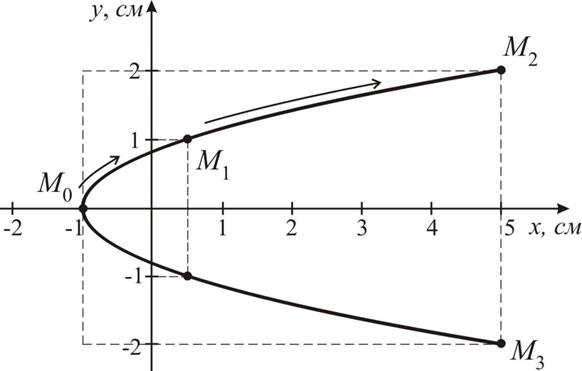
Рис. 1.10
2. Вычислим координаты точки для фиксированного времени.
Для этого подставим значение ![]() в (а) и вычислим
соответствующую координату:
в (а) и вычислим
соответствующую координату:
при ![]() :
: ![]() (см);
(см);
![]() ;
;
при ![]() с:
с: 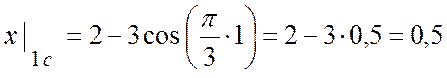 (см);
(см);
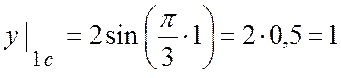 (см).
(см).
3. Вычислим скорость ![]() точки
М для
точки
М для ![]() с.
с.
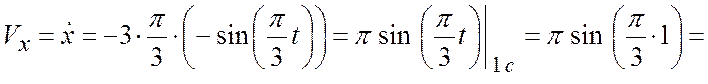
![]() (см/c);
(см/c);
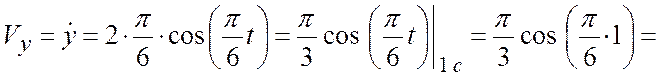
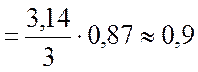 (см/c);
(см/c);
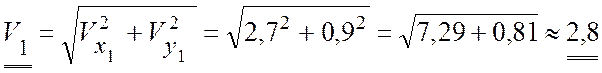 см/с;
см/с;
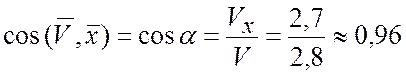 ,
,
![]() .
.
Откладываем проекции скорости ![]() на
графике (рис. 1.11).
на
графике (рис. 1.11).
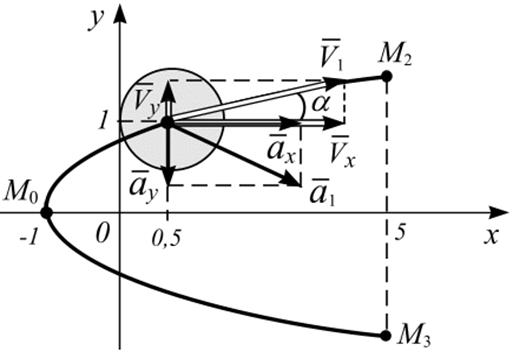
Рис. 1.11
4.Вычислим ускорение ![]() точки М для
точки М для ![]() с:
с:
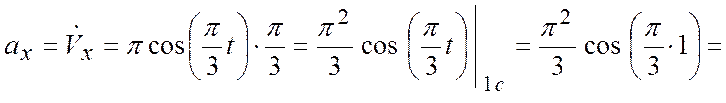
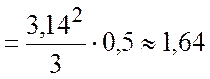 (см/c2);
(см/c2);
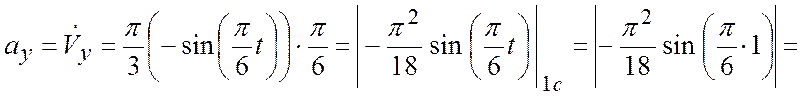
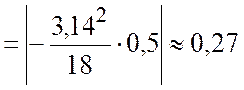 (см/c2);
(см/c2);
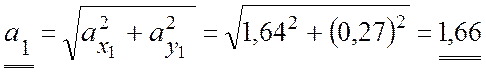 (см/c2);
(см/c2);
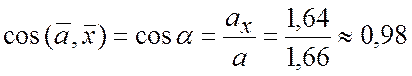 ,
,
![]()
Откладываем проекции ускорения ![]() на
графике (рис. 1.11).
на
графике (рис. 1.11).
Ответ:
· траектория точки парабола 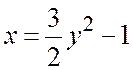 ;
;
· положение точки на траектории определяется
координатами ![]() ,
, ![]() ;
;
·
скорость точки ![]() см/c;
ускорение точки
см/c;
ускорение точки ![]() см/c2.
см/c2.
·
|
J |
Вспомни теорию |
|
Прямая
задача - по
заданному уравнению движения ![]() требуется
вычислить скорость и ускорение точки:
требуется
вычислить скорость и ускорение точки:
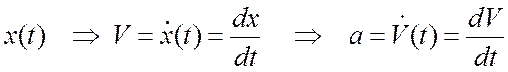 .
.
Если ![]() и
и ![]() имеют
один знак, то вектор скорости и вектор ускорения направлены в одну сторону, тогда
движение будет ускоренным; если в противоположные – замедленным.
имеют
один знак, то вектор скорости и вектор ускорения направлены в одну сторону, тогда
движение будет ускоренным; если в противоположные – замедленным.
Задача 1.5.
Прямолинейное движение точки М задано уравнением ![]() . Вычислить скорость и
ускорение точки М в момент времени
. Вычислить скорость и
ускорение точки М в момент времени 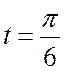 с.
с.
Решение.
Траекторией движения точки является отрезок на прямой ![]() (м)
(рис. 1.12). Точка начинает движение вправо из координаты
(м)
(рис. 1.12). Точка начинает движение вправо из координаты ![]() (
(![]() )
до координаты
)
до координаты ![]()
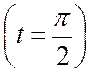 ,
далее вектор скорости меняет направление, и точка движется влево до координаты
,
далее вектор скорости меняет направление, и точка движется влево до координаты ![]()
![]() и
т.д. В момент времени
и
т.д. В момент времени 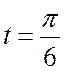 с точка М
имеет координату
с точка М
имеет координату
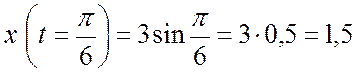 м.
м.
Имеем: 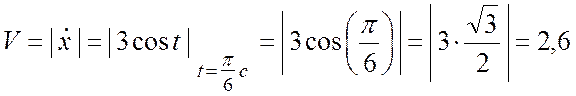 (м/с);
(м/с);
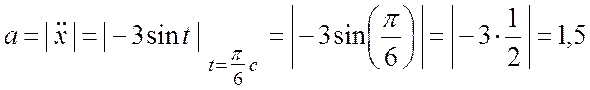 (м/с2).
(м/с2).
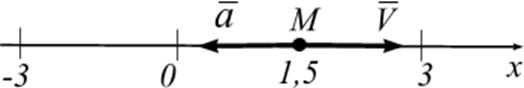
Рис. 1.12
Знаки производных определяют направление векторов ![]() и
и ![]() ,
поэтому точка в этот момент времени движется замедленно, вектор скорости и
вектор ускорения направлены по оси
,
поэтому точка в этот момент времени движется замедленно, вектор скорости и
вектор ускорения направлены по оси ![]() в
противоположные стороны (рис. 1.12).
в
противоположные стороны (рис. 1.12).
Ответ: ![]() (м/с);
(м/с); ![]() (м/с2).
(м/с2).
|
J |
Вспомни теорию |
|
Обратная задача -
задано ускорение движущейся точки ![]() и требуется
вычислить скорость точки и уравнение движения точки
и требуется
вычислить скорость точки и уравнение движения точки ![]() :
:
![]() .
.
Ускорение точки связано со скоростью, скорость с координатой дифференциальными уравнениями:
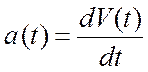 ,
,
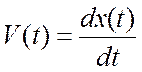 . (2)
. (2)
При решении дифференциальных уравнений (2) разделяют переменные
![]()
![]() (3)
(3)
и интегрируют (3) с учетом начальных условий задачи, т.е. значений координаты и скорости в начальный момент времени:
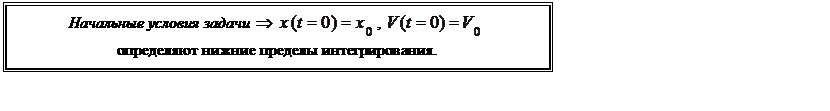
![]()
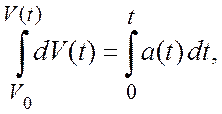
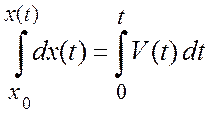 .
.
![]() При интегрировании уравнений (3)
нижние пределы интегрирования соответствуют значениям интегрируемых величин
в начальный момент времени, т.е. начальным условиям задачи, верхние пределы
интегрирования соответствуют значению интегрируемых величин при текущем
времени t.
При интегрировании уравнений (3)
нижние пределы интегрирования соответствуют значениям интегрируемых величин
в начальный момент времени, т.е. начальным условиям задачи, верхние пределы
интегрирования соответствуют значению интегрируемых величин при текущем
времени t.
Задача 1.6.
Точка движется вдоль оси ![]() с ускорением
с ускорением ![]() . В начальный момент времени (
. В начальный момент времени (![]() )
) ![]() ,
, ![]() м/c. Вычислить скорость точки через
м/c. Вычислить скорость точки через ![]() с.
с.
Решение. Ускорение и скорость точки связаны между собой
дифференциальным уравнением с разделенными переменными
![]() .
(а)
.
(а)
Начальные условия задачи: ![]() (м/c).
(м/c).
Подставив значение ускорения в (а), получим:
![]()
Взяв от обеих частей
равенства определенный интеграл с учетом начальных условий задачи, получим
величину скорости точки через ![]() с:
с:
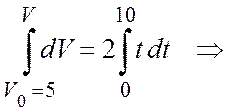
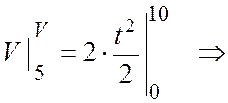
![]()
![]()
![]() (м/с).
(м/с).
Ответ:![]() (м/с).
(м/с).
1.3. Естественный способ задания движения точки
|
J |
Вспомни теорию |
|
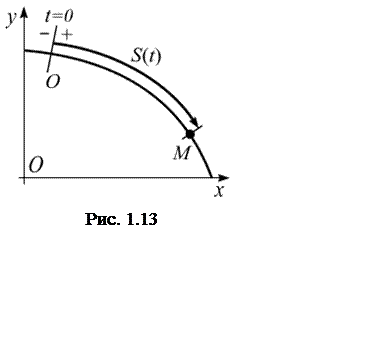 При естественном способе задания
движения точки известно (рис. 1.13):
При естественном способе задания
движения точки известно (рис. 1.13):
· траектория точки;
· начало и направление движения, т.е. направление увеличения дуговой координаты;
· уравнение
движения ![]() где S
– дуговая координата.
где S
– дуговая координата.
Скорость и ускорение точки. При
естественном способе задания движения точки в плоскости применяют оси
естественного трехгранника ![]() ,
, ![]() , которые жестко связываются с точкой
М и движутся вместе с ней. Плоскость
, которые жестко связываются с точкой
М и движутся вместе с ней. Плоскость ![]() ,
, ![]() называется соприкасающейся
плоскостью.
называется соприкасающейся
плоскостью.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.