Векторный способ задания движения точки. Координатный способ задания движения точки, страница 6

·  разделяем переменные в дифференциальном уравнени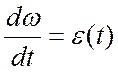и  или 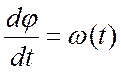 и интегрируем по времени дифференциальные уравнения с разделенными переменными с учетом начальных условий задачи, вычисляем угловую скорость твердого тела  или уравнение вращения твердого тела ;

·  вычисляем скорость любой точки твердого тела , ускорение любой точки твердого тела .

J	Задачи для самостоятельного решения
		1. Угловая скорость  зубчатого колеса  (диаметр колеса D= 50мм) равна  рад/с. Каким должен быть диаметр зубчатого колеса , находящегося с колесом  во внутреннем зацеплении, угловая скорость которого в три раза больше угловой скорости колеса ?
2.  Станок со шкивом  приводится в движение из состояния покоя бесконечным ремнем от шкива  электромотора; радиусы шкивов  см;  см, после пуска в ход электромотора его угловое ускорение  с-2. Пренебрегая скольжением ремня по шкивам, вычислить, через какое время угловая скорость станка будет  рад/с.
			3. Вал радиусом  см приводится во вращение гирей , привешенной к нему на нерастяжимой нити. Движение гири задано уравнением , где  - расстояние гири от места схода нити с поверхности вала,  - время в секундах.Вычислить угловую скорость и угловое ускорение вала, полное ускорение точки на его поверхности в момент времени .
				4. Механизм, состоящий из двух составных дисков, приводится в движение гирей, подвешенной к одному из дисков на нерастяжимой нити. Движение гири задано уравнением  (м). Вычислить скорость точки А и ускорение точки В через 1 с, если  м,  м,  м,  м.
				5.  Механизм, состоящий из двух дисков, приводится в движение рейкой, находящейся в зацеплении с первым диском. Движение рейки задано уравнением  (м).Вычислить скорость точки А и ускорение точки В через 3 с, если  м,  м,  м.
					6.  Механизм, состоящий из двух ступенчатых дисков, приводится в движение грузом, подвешенным к диску 2 нерастяжимой нитью. Движение гири задано уравнением  (м). Вычислить скорость точки А и ускорение точки В через 2с, если  м,  м,  м,  м.
7.  Вычислить скорости точек А, С и ускорение точки В через  с, если задано уравнение движения груза  (см);  см,  см,  см,  см,  см,  см.
8.  Вычислить скорости точек А, С и ускорение точки В через  с, если задано уравнение движения зубчатой рейки  (см);  см,  см,  см,  см,  см,  см.
9. Вычислить скорость точки А и ускорение точек С и В через  с, если уравнение движения груза 3, если  (см),  см;  см;  см;  см;  см;  см.

3. Сложное движение точки

J

Вспомни теорию

Абсолютная скорость. Абсолютная скорость точки равна геометрической сумме ее относительной и переносной скорости:

.

Здесь  - скорость относительного движения,

 – скорость переносного движения.

Вычисление относительной скорости . Скорость вычисляется в зависимости от способа задания относительного движения.

А. Движение точки в ее относительном движении задано координатным способом, т.е. в декартовой системе координат задают  функции  тогда    

                        ,   .

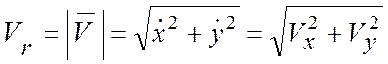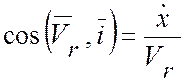Б. Движение точки в ее относительном движении задано естественным способом, т.е. задана траектория движения точки и функциональная зависимость дуговой координаты со временем . Выбирают yнаправление  осей естественного трехгранника τ, n.

Тогда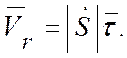                                                            

Вычисление переносной скорости. Рассмотрим частные случаи вычисления переносной скорости.

1.  Подвижная система координат движется поступательно со скоростью . В этом случае 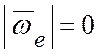 и переносная скорость совпадает со скоростью подвижной системы координат, т.е.

.

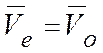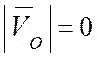2.  Подвижная система координат вращается относительно неподвижной оси c угловой скоростью . В этом случае , тогда переносная скорость:

.

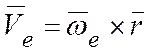Абсолютное ускорение. Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.

.

Здесь:   – ускорение относительного движения,

 – переносное ускорение,

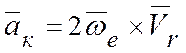 – ускорение Кориолиса.

Вычисление относительного ускорения. Относительное ускорение вычисляется в зависимости от способа задания относительного движения.

А.   При координатном способе задания относительного движения точки М:

;   ;   .

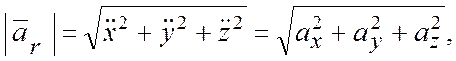
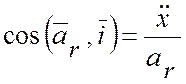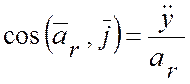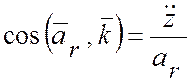Б.  При естественном способе задания движения:

,   ,   ,

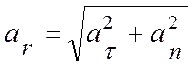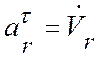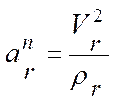здесь  – радиус кривизны относительной траектории точки М.

Вектор относительного ускорения расположен в соприкасающейся плоскости относительного движения.

Вычисление переносного ускорения. Переносное ускорение вычисляется в зависимости от способа задания относительного движения и движения подвижной системы координат.

А.  Подвижная система координат движется поступательно. В этом случае 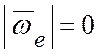 и 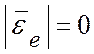, следовательно, переносное ускорение точки М:

.

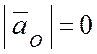Б. Подвижная система координат вращается относительно неподвижной оси с угловой скоростью  и угловым ускорением . В этом случае , тогда переносное ускорение

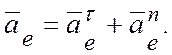
Если точка движется по окружности радиусом h, то здесь:

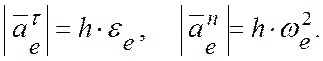
Вектор переносного ускорения расположен в соприкасающейся плоскости переносного движения, т.е. в плоскости, перпендикулярной оси вращения.

Вычисление ускорения Кориолиса. Модуль ускорения Кориолиса:

.

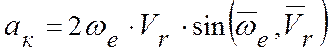Вектор ускорения Кориолиса направлен перпендикулярно вектору угловой скорости , т. е. .

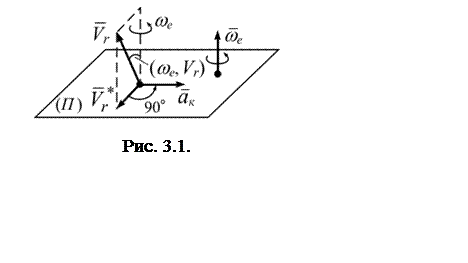Правило Жуковского: чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости  на плоскость, перпендикулярную , повернуть на  вокруг оси вращения  в направлении дуговой стрелки вращения (рис.3.1).