Динамический анализ и синтез механизмов

6. ДИНАМИЧЕСКИЙ АНАЛИЗ И СИНТЕЗ МЕХАНИЗМОВ

6.1. Теоретическая часть

Динамический анализ и синтез механизма заключается в определении момента инерции  по заданным условиям движения (т. е. по заданной величине коэффициента неравномерности δ).

В пособии изложены методы решения задачи проектирования маховика, а также определения закона изменения кинематических параметров (угловой скорости) с учетом особенностей, свойственных установившемуся движению.

6.1.1. Основные режимы движения механизма

Процесс движения механизма в общем случае состоит из трех фаз: разгон, установившийся режим и торможение (выбег) (рис. 6.1).

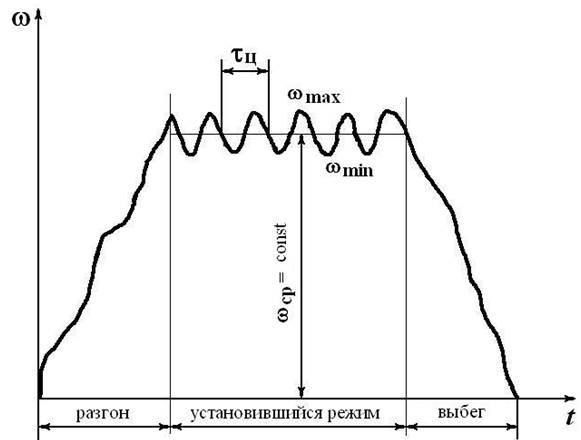
Рис. 6.1. Периоды движения механизма

Фаза разгона характеризуется увеличением скорости звена приведения. Это наблюдается при пуске механизма в ход или переводе его с меньшей скорости на большую.

Установившийся режим характерен для машин, выполняющих циклически повторяющийся рабочий процесс. При установившемся режиме скорость звена приведения является периодической функцией времени , период которой равен одному циклу. Причиной являются периодический характер действия сил и моментов, приложенных к механизму, а также периодическое изменение приведенного момента инерции механизма. Среднее значение угловой скорости поддерживается на постоянном уровне. За цикл установившегося движения , то есть работа движущих сил полностью затрачивается на преодоление сил полезного и вредного сопротивлений.

Режим торможения – это переход от установившегося движения к состоянию покоя, скорость звена приведения уменьшается.

Характерным режимом работы машины является установившееся движение. В курсовом проекте рассматривается режим установившегося движения.

При теоретическом исследовании и инженерных расчетах любой реальной механической системы составляют её физическую модель, так как полное описание процессов, происходящих в реальной механической системе, не представляется возможным и необходимым. При решении задач динамики используют динамическую модель.

Наиболее простой динамической моделью механизма служит модель, основанная на допущении, что звенья абсолютно жесткие (не деформируются), отсутствуют зазоры в кинематических парах и погрешности изготовления.

Вследствие неизбежных расхождений между реальной машиной и её динамической моделью действительные законы движения выходных звеньев отличаются от идеальных. Расхождение между действительными и идеальными законами движения называются динамическими ошибками. Определение их составляет одну из основных задач динамического анализа машины.

Механизм заменяют эквивалентной динамической моделью (расчетной схемой), состоящей из одного вращающегося звена – звена приведения, которое имеет переменный приведенный момент инерции механизма  и находится под действием переменного суммарного приведенного момента  движущих сил и сил сопротивления. В качестве звена приведения обычно принимается начальное (ведущее) звено (рис. 6.2).

Приведенный момент инерции , приведенные моменты движущих сил  и сил сопротивления  зависят от положения механизма, которое определяется положением ведущего звена, например, координатой j при одной степени подвижности механизма.

Таким образом, приведение сил и масс позволяет упростить решение динамической задачи, так как определение закона движения механизма сводится к определению закона движения одной точки или одного звена.

Поскольку приведение сил осуществляется из условия равенства элементарных работ, а приведение масс – из условия равенства кинетических энергий, то закон движения звена приведения, полученный в результате исследования динамической модели, будет таким же, как и в реальном механизме.

Математическое описание динамической модели машины осуществляется составлением соответствующих уравнений.

6.1.2. Приведенный момент инерции механизма

Приведенный момент инерции механизма  представляет собой момент инерции, которым должно обладать звено приведения относительно оси его вращения, чтобы кинетическая энергия этого звена равнялась сумме кинетических энергий всех звеньев механизма.

Из условия эквивалентности динамической модели и механизма (равенства их кинетических энергий) определяется приведенный момент инерции механизма . Этим моментом инерции обладает звено приведения в рассматриваемом положении механизма:

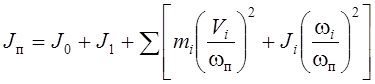,                             (6.1)

где   – момент инерции самого звена приведения;   – приведенные моменты инерции звеньев, которые связаны со звеном приведения постоянным передаточным отношением, т. е. не зависят от положения механизма (ротор электродвигателя, зубчатые, цепные передачи и т. д.);  – угловая скорость звена приведения, рад/с;   – масса i-го звена, кг, и скорость его центра масс, мс^-1, взятая из плана скоростей;  –  момент инерции массы относительно центра тяжести, кг·м², и угловая скорость i-го звена, с^-1.