Динамический анализ и синтез механизмов, страница 12

5) на основании ранее построенных графиков  и  J_п(j) строим диаграмму «энергомасс» ΔТ(J_п). Диаграмма «энергомасс» строится графическим исключением параметра j из диаграмм  и  J_п(j) (рис. 6.14,в).

Построение графика «энергомасс» выполнено с помощью прямой, наклоненной под углом 45°. На эту прямую горизонтальными линиями переносят ординаты точек кривой . Через полученные точки на этой прямой проводят вертикальные линии, на которых находят точки пересечения с горизонтальными прямыми, проведенными через соответствующие точки графика приведенного момента инерции J_п(j) группы звеньев.

Находим координатные оси новой системы, в которой диаграмма «энергомасс» соответствует механизму с заданным коэффициентом неравномерности δ = 0,03 при средней угловой скорости ω_п=15 рад/с. К кривой диаграммы проводятся касательные под углами ψ_max  и ψ_min, соответствующие максимальной и минимальной угловым скоростям звена приведения с маховиком. Для этого находим тангенсы максимального и минимального углов наклона касательных к диаграмме «энергомасс»:

,

,

,

.

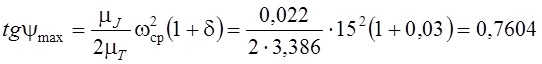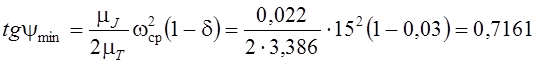Для проведения касательных углы y_max  и y_min не вычисляются, так как удобнее пользоваться их тангенсами путем построения прямоугольных треугольников с известным соотношением катетов. Проведя касательные под вычисленными углами к диаграмме «энергомасс» находим точку их пересечения.

Точка пересечения касательных является искомым центром координат. Если начало координат находится вне чертежа, то используют отрезок , отсекаемый касательными на оси кинетических энергий . Из чертежа видно как определяется длина отрезка . Этот отрезок изображает в масштабе  наибольшее изменение кинетической энергии маховика в течение периода его установившегося движения.

,

,

,

 находится измерением,

.

По чертежу , тогда . На основании этой формулы момент инерции маховика, установленного на валу звена приведения (кривошипа), будет

.

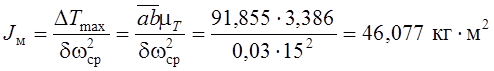6.4.3. Определение момента инерции методом Е.М. Гутьяра

Последовательность выполнения в пп. 1–4 совпадает с последовательностью, описанной для способа Мерцалова – Рериха (6.4.1).

Одну под другой строят диаграммы  и J_п(j) (рис. 6.14, а, б). Вычитая из «избыточной» энергии механизма ΔТ максимальную и минимальную энергию звеньев, получают две диаграммы кинетических энергий маховика  и  (рис. 6.16).

Значения ординат диаграмм  и  для второго положения механизма определяется следующим образом:

,

, где     ;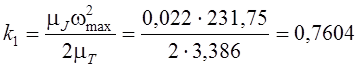

;

;

.

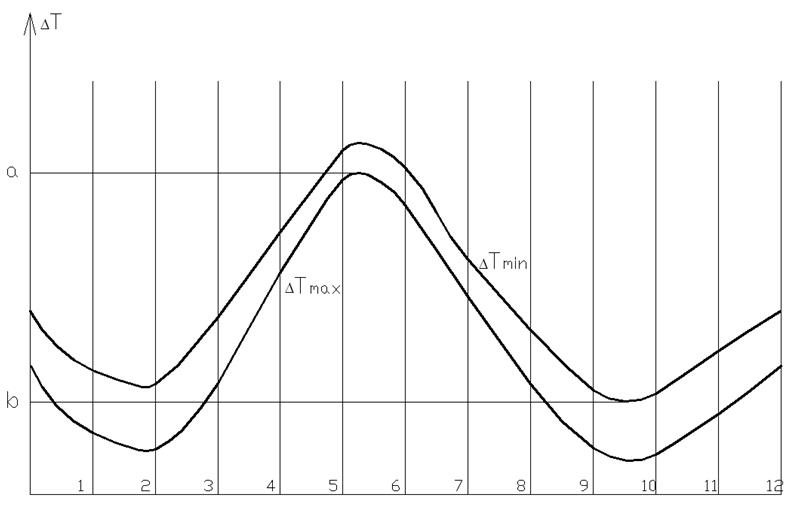
Рис. 6.16. Диаграмма максимального и минимального изменения кинетической энергии маховика, μ_ΔTм = 3,0076 Нм/мм

Полученные данные заносят в табл. 6.4.

Таблица 6.4

Результаты определения приращения кинетической энергии

По вычисленным значениям  и  строится диаграмма в масштабе

.

Проводим горизонтальные прямые, касающиеся первой кривой в т. a наибольшего максимума, второй кривой в т. b наименьшего минимума. Прямые отсекают на оси ординат отрезок .

.

Момент инерции маховика подсчитывается по формуле

.

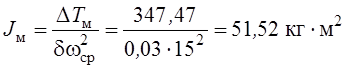6.5. Габаритные размеры и масса маховика

Момент инерции маховика и его масса зависят от его местоположения в кинематической цепи механизма. Чем выше частота вращения вала, на котором установлен маховик, тем меньше его размеры при вычисленном моменте инерции J_п группы звеньев, обеспечивающем движение начального звена с номинальной средней угловой скоростью и заданным коэффициентом неравномерности движения δ.