Динамический анализ и синтез механизмов, страница 13

Маховик выполняется в форме колеса со спицами со средним диаметром D_ср  и шириной b (рис. 6.17). Предполагая, что масса обода m_об равномерно распределена по окружности среднего диаметра обода D_ср, можно использовать формулу для определения момента инерции тонкого кольца

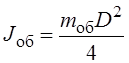,                    (6.61)

где – масса обода, кг; ρ – плотность, кг/м³; ; ; ; .

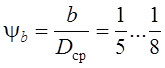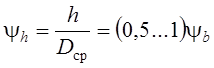Подставляя эти формулы в выражение (6.61), можно найти средний диаметр обода

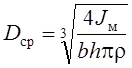.                                          (6.62)

Для стальных маховиков можно принять ρ = 7800 кг/м³, для чугунных – 7100 кг/м³.

Определим средний диаметр обода. Пусть ρ = 7800 кг/м³. Выберем ψ_b = 0,2, тогда b = 0,2D_ср, h = 0,1D_ср. Примем  – среднее значение по трем методам определения момента инерции маховика. Найдем средний диаметр обода

.

,

.

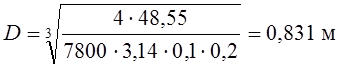6.6. Определение угловой скорости звена приведения

после установки маховика

При кинематическом исследовании машины предполагалось, что главный вал вращается равномерно с угловой скоростью . В действительности угловая скорость ω главного вала является переменной величиной.

Зная момент инерции маховика, а также то положение машины, в котором ω = ω_max, либо ω = ω_min, можно определить значения угловой скорости главного вала для любых положений машины внутри периода установившегося движения.

Истинная угловая скорость вычисляется по формуле

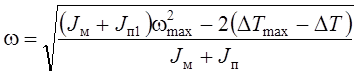.                            (6.63)

Последовательность выполнения работы:

1.  Пользуясь диаграммой  (см. рис. 6.14), определяем значение  для положения машины, в котором ω = ω_max, а также значения ΔT для ряда положений машины внутри периода установившегося движения. На рис. 6.11 ординаты, измеряющие величину ΔT₁ на диаграммах , соответствуют абсциссам OA.

2.  Подсчитываем ряд значений J_п для тех положений машины, для которых подсчитаны ΔT в п. 6.3.6. Можно также использовать те значения J_п, которые ранее были определены при подсчете  (способ Мерцалова-Рериха) или значений  и  (способ Гутьяра).

3.  Определяем значения ω для тех же положений по формуле

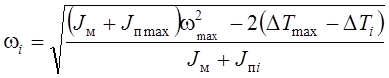, где ω_i – истинная угловая скорость кривошипа в i положении; J_м – момент инерции маховика; J_п2 – приведенный момент инерции звеньев механизма в положении, соответствующем максимальной угловой скорости (в нашем случае – положение 2); J_пi – приведенный момент инерции в положении i (берем по данным табл. 6.5); ω_max – максимальная угловая скорость кривошипа, определяемая по формуле 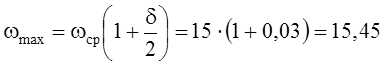; ΔT₅ – приращение кинетической энергии всей машины, соответствующей максимальной угловой скорости кривошипа ; y₅ – ордината диаграммы , соответствующая ΔT₅ (ордината в  положении 5); μ_T – масштаб оси ординат диаграммы  (μ_T=3,386 Нм/мм); ΔT_i – величина приращения кинетической энергии в i положении, равная ; y_i – ордината диаграммы (табл. 6.5).

4. По значениям истинной угловой скорости строим диаграмму изменения угловой скорости кривошипа  за период установившегося движения в масштабе , . Вычислим угловую скорость в  положении 2.

.

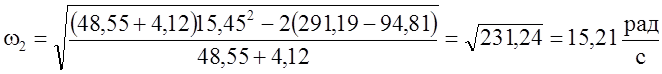Полученные результаты заносим в табл. 6.5.

Таблица 6.5

Величины угловых скоростей кривошипа

По данным табл. 6.5 построим диаграмму изменения угловой скорости (рис. 6.18).

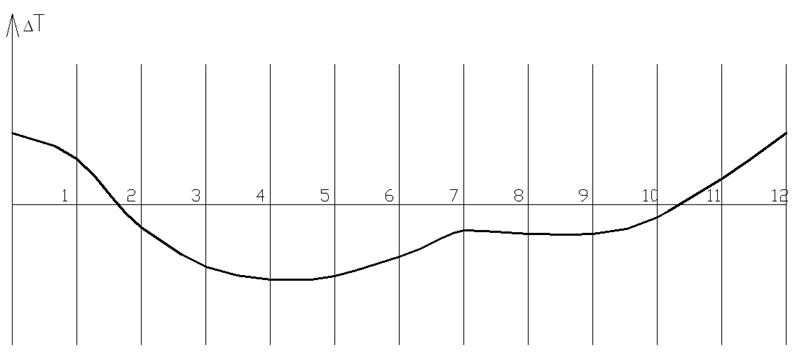
Рис. 6.18. Диаграмма изменения угловой скорости кривошипа, μ_ω=3,386 Нм/мм