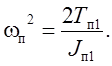Динамический анализ и синтез механизмов, страница 3

                                                  (6.10)

Величина угловой скорости ω колеблется внутри цикла между значениями ω_max и ω_min. Вследствие этого колеблется и кинетическая энергия Т₁, проходя через максимальное и минимальное значения. Момент инерции J_п1 звена приведения имеет постоянную величину, не зависящую от положения механизма,

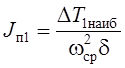,                                               (6.11)

где ΔТ_1наиб – наибольший перепад кинетической энергии с постоянным приведенным моментом инерции J_п1.

Формула (6.11) является расчетной для определения момента инерции звена приведения, необходимого для обеспечения его вращения с заданной неравномерностью, выраженной коэффициентом δ. Чем меньше заданное значение δ, т. е. чем равномернее должно вращаться звено приведения, тем больше получается величина момента инерции J_п1, тем массивнее должен быть маховик.

6.1.5 Уравнение движения машины

Используем уравнение движения машины в форме уравнения изменения кинетической энергии машины:

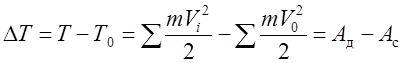,                        (6.12)

,                                                     (6.13)

где ΔТ – приращение кинетической энергии машины, соответствующее повороту главного вала из начального положения в положение, определяемое углом j; Т₀ – кинетическая энергия машины в начальном положении; Т – кинетическая энергия машины в положении, определяемом углом j; А_д – работа всех движущих сил; А_с – работа всех сил сопротивления.

Из указанных формул (6.8) и (6.13) имеем

                                           (6.14)

6.1.6. Основные характеристики установившегося

движения машины

Периодом установившегося движения машины называют такой наименьший промежуток времени, по истечении которого положения и скорости всех точек машины начинают изменяться в той же последовательности, в какой они изменялись в течение этого промежутка времени.

Энергия, подводимая к механизму и потребляемая им, в каждый момент времени не равны между собой (рис. 6.5). Их равенство возможно лишь при установившемся движении за время цикла (внутри цикла равенства нет).

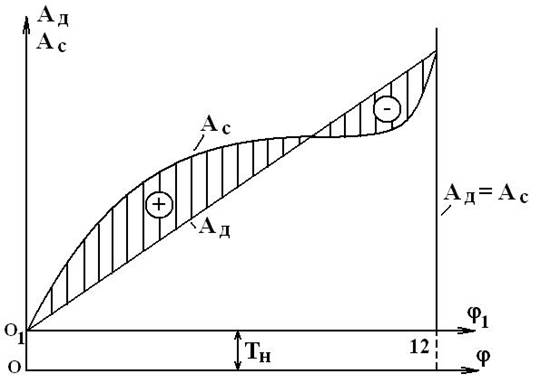
Рис. 6.5. Диаграмма работ движущих сил и сил сопротивления

Установившееся движение имеет место только в том случае, когда сумма работ за цикл всех сил, приложенных к механизму, равна нулю: .

Так как работа сил тяжести за цикл равна нулю, то это равенство будет выполняться, если работа движущих сил за цикл равна работе сил сопротивления за цикл (по абсолютной величине):

                                                (6.15)

Уравнение (6.15) является основным энергетическим уравнением установившегося движения. Из него вытекает, что приращения кинетической энергии механизма за цикл не происходит (ΔТ_ц= 0), следовательно, угловая скорость звена приведения в начале и в конце цикла одинакова.

При установившемся режиме движения угловая скорость ω звена приведения хотя и остается в среднем постоянной, но внутри цикла изменяется, проходя через максимальное ω_max и минимальное ω_min значения. Неравномерность вращения оценивается коэффициентом неравномерности δ:

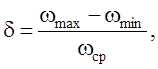                                               (6.16)

где  – средняя угловая скорость за цикл, с^-1; n – число оборотов главного вала в минуту.

Из уравнения (6.16) видно, что δ характеризует размах колебаний угловой скорости по отношению к ее среднему значению. Чем меньше δ, тем относительно меньше размах колебаний, тем спокойнее вращается звено приведения.

Коэффициент неравномерности – величина весьма малая, что позволяет принять среднюю величину угловой скорости приближенно равной среднему арифметическому из ее максимального и минимального значений .

Величины максимальной и минимальной угловой скорости

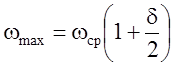,                                       (6.17 а)

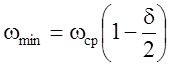.                                       (6.17 б)

Как видно из уравнений (6.17) отличие ω_max  и ω_min составляет ± δ/2, т. е. обычно не более ±2%. Следовательно, амплитуда колебаний угловой скорости ω не превышает в большинстве случаев 2% от ее среднего значения.

6.2. Определение момента инерции маховика

и его махового момента