Динамический анализ и синтез механизмов, страница 7

На траектории движения точки A отмечаем крайние положения A₀ и A₅, которые соответствуют крайним положениям механизма.

Крайними положениями механизма называются положения, где скорость выходного звена (ползуна D) равна нулю.

Крайними положениями исследуемого механизма с вращательным движением начального звена могут быть такие положения, когда кривошип и шатун то вытягиваются, то складываются в одну линию. Для кулисного механизма с качающейся кулисой крайними могут являться такие положения, когда кривошип и кулиса взаимно перпендикулярны.

Начиная от точки A₀ – начала рабочего хода ползуна D – окружность радиуса OA делим на 12 равных частей. Точки деления обозначаем A₁, A₂, A₃ и т.д. в направлении вращения кривошипа.

Определяем начальное и конечное положение выходного звена (ползуна D). Строим над траекторией движения ползуна график действия сил полезного сопротивления. По заданному графику сил полезного сопротивления и величине силы  на листе строим график силы в функции положения ползуна , согласовав абсциссу с ходом H_п ползуна на кинематической схеме, вычерченной в масштабе длины . Подобное построение позволяет  перенести на график разметку траектории ползуна и найти значение силы полезного сопротивления в каждой фиксированной позиции механизма.

6.3.3. Построение плана скоростей для каждого из 12 положений

Начинаем построение плана скоростей с входного звена (рис. 6.11).

Если начальное звено механизма совершает вращательное движение, то скорость его любой точки, например  A, определяется по формуле

,                               (6.53)

где  – скорость точки A, м/с;  – кратчайшее расстояние от оси вращения до точки A, м;  – угловая скорость звена OA, рад/с.

а)

б)

Рис. 6.11. План скоростей, μl = 0,036 м/с·мм: а – для второго положении; б – для восьмого положения

Скорость точки A перпендикулярна прямой OA () и может быть изображена на плане скоростей вектором , модуль которого будет 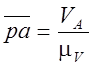, где масштабный коэффициент скорости

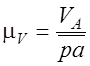,                                               (6.54)

где p – полюс плана скоростей; a – одноименная точка на звене.

Выбрав длину  такой, чтобы длина наименьшего вектора плана скоростей могла быть измерена с погрешностью не более 5%, найдем масштабный коэффициент плана скоростей 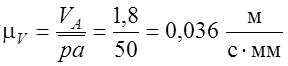. Рекомендуемая длина вектора  - 50–100 мм.

Для определения скорости точки B раскладываем плоскопараллельное движение звена 2 на переносное  (поступательное вместе с т. A) и относительное (вращательное вокруг т. А). С другой стороны, т. В находится в относительном движении вокруг неподвижной т. О₁. Поэтому необходимо записать два векторных уравнения, графическое решение которых дает искомую скорость:

, где – переносная скорость, ее вектор изображен на плане;  – относительная скорость, ее вектор перпендикулярен звену АВ.

, где   – переносная скорость точки О₁, принадлежащей неподвижной стойке ();  – относительная скорость, ее вектор перпендикулярен звену ВО₁.

Эту систему из двух уравнений решаем графически. Через т. А проводим линию, перпендикулярную АВ, а через полюс р – линию, перпендикулярную ВО₁, до их пересечения в т. В. Векторы и изображают искомые скорости  и .

Следует заметить, что направление вектора относительной скорости на плане не соответствует последовательности букв в индексе обозначения относительной скорости. Например, вектор направлен не от точки «b» к точке «а», а в противоположном направлении, согласно векторному уравнению , т. е. .

Скорость точки D₃ звена 3 определяем, используя теорему подобия. Точка на плане делит вектор-отрезок в таком же отношении, как соответствующая точка делит звено механизма.

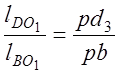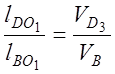, ,  откуда

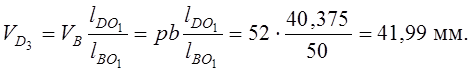
Скорость т. K, принадлежащей кулисе,

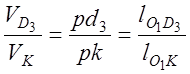, следовательно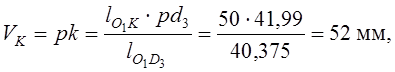

где  – размеры звена, измеренные по чертежу, мм.

Отрезок pd₃ откладываем от полюса р на продолжении отрезка , так как обе точки находятся на одном звене и вращаются вокруг неподвижной т. О₁.