Физика \ Физика

Динамический анализ и синтез механизмов, страница 11

По вычисленным значениям приведенного момента инерции строится его диаграмма в масштабе (рис. 6.14, а).

.

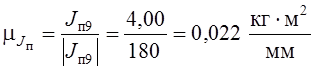Значение масштаба принимать таким образом, чтобы обеспечивалась достаточная точность последующих вычислений.

6.4. Определение момента инерции маховика

Находится момент инерции маховика. Искомое значение Jм, обеспечивающего заданный коэффициент неравномерности движения δ, можно определить по формуле

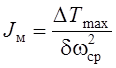,                                                 (6.58)

где  ΔТmax – наибольший перепад кинетической энергии звеньев с постоянным приведенным моментом инерции Jм.

Для определения ΔТmax могут быть использованы методы Ф. Виттенбауэра,  Е. М. Гутьяра или метод Н. И. Мерцалова и К. Э. Рериха.

6.4.1 Определение момента инерции маховика методом Н. И. Мерцалова и К. Э. Рериха

Чтобы определить момент инерции маховика по методу Н. И. Мерцалова необходимо:

1)  построить диаграмму суммарного приведенного момента сил сопротивления  (см. п. 6.3.4);

2)  построить диаграмму  работ сил сопротивления способом графического интегрирования и диаграмму работ  движущих сил (см. п. 6.3.5);

3)  построить диаграмму «избыточной» энергии механизма ΔТ(j) (см. п. 6.3.6);

4)  построить диаграмму приведенного момента инерции Jп(j) (см. п. 6.3.7);

5)  построить диаграмму изменения кинетической энергии ΔТ(j) звеньев с постоянным приведенным моментом инерции Jп. Проводим две горизонтальные прямые, касающиеся кривой ΔТ(j) в точках наибольшего максимума а и наименьшего минимума b и отсекаем этими прямыми отрезок [ab] на оси ординат (рис. 6.15);

6)  подсчитываем приближенное значение момента инерции маховика  Jп  по уравнению (6.58).

ΔТм можно получить по формуле

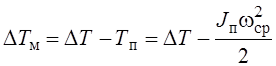, где Тп – кинетическая энергия звеньев с переменным приведенным моментом инерции Jп, определяемая приближенно по средней угловой скорости звена приведения ωср (как меньшая часть полной кинетической энергии механизма).

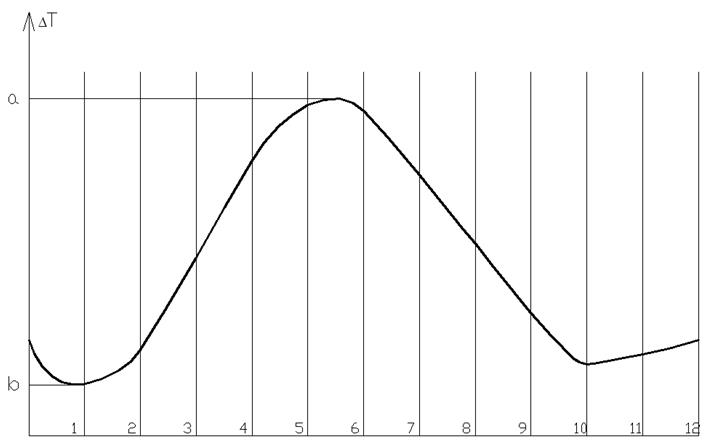
Рис. 6.15. Диаграмма изменения среднего значения кинетической энергии маховика за цикл, μΔTм = 3,8 Нм/мм

Это выражение можно записать в виде

,                                   (6.59)

где 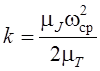.                                                                                                    (6.60)

Из выражения (6.59) следует, что для построения графика  нужно от кривой  с диаграммы «избыточной» энергии механизма для соответствующих положений механизма отложить вниз ординаты , измеренные на графике  и умноженные на постоянный коэффициент k.

Для второго положения механизма ордината определится следующим образом:

 ,

.

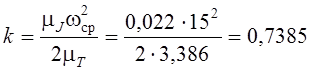Результаты вычислений для всех положений приведены в табл. 6.3. При вычислении ординаты  измеряются в миллиметрах по соответствующей диаграмме со знаком «+» или «–».

Таблица 6.3

Результаты определения кинетической энергии

 звена приведения

i

, мм

, мм

k

, Н·м

, мм

0

–

–

–

–

–

2

28

185,42

0,7383

-386,69

-97,02

3-12

–

–

–

–

–

Масштабный коэффициент кинетический энергии маховика

.

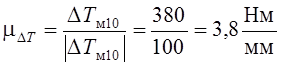Обозначим а и b максимум и минимум диаграммы соответственно. Наибольший перепад кинетической энергии выразится отрезком  в масштабе . По графику  (рис. 6.15) находится максимальное изменение кинетической энергии маховика:

,

.

Момент инерции маховика определяется по формуле

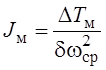, где δ – коэффициент неравномерности движения.

.

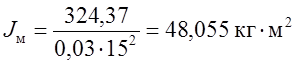6.4.2.  Определение момента инерции маховика

методом Ф. Виттенбауэра

Последовательность выполнения в пп. 1–4 совпадает с последовательностью, описанной для способа Мерцалова – Рериха (6.4.1). Далее поступаем так:

Скачать файл