Динамический анализ и синтез механизмов, страница 4

В процессе проектирования машины определяются все параметры ее звеньев, позволяющие подсчитать значение приведенного момента инерции J_п для всех положений машины. Однако этот момент инерции часто оказывается недостаточным для обеспечения (при заданном значении ω_ср) границ колебания угловой скорости ω главного вала, заданных коэффициентом δ. В этом случае возникает задача подбора дополнительно маховика с таким моментом инерции J_м, при котором эти границы обеспечиваются.

Для определения момента инерции маховика применяют способы Н.И. Мерцалова и К. Э. Рериха, метод Е. М. Гутьяра или Ф. Виттенбауэра.

Рассматриваемый механизм имеет степень подвижности, равную единице, поэтому положение механизма задается одним параметром. В качестве такого параметра выберем угол поворота главного вала машины j, отсчитанный от крайнего положения.

6.2.1. Метод Ф. Виттенбауэра

Метод Ф. Виттенбауэра основан на применении диаграммы «энергомасс». Для ее построении сначала строят графики J_п(j) и ΔТ(j). Затем строят диаграмму ΔТ(ΔJ_п). Построение этой диаграммы по графикам функций J_п(j) и ΔТ(j) производят исключением параметра j. Вертикальная ось новой системы координат представляет собой кинетическую энергию Т механизма, горизонтальная – приведенный момент инерции J_п. Кривая ΔТ(ΔJ_п) должна иметь замкнутый вид, так как она построена для установившегося режима. Кинетическая энергия всего механизма . Приведенный момент инерции . Величины начальной кинетической энергии Т₀ механизма и момента инерции J_м маховика неизвестны. Поэтому на характер кривых J_п(j) и ΔТ(j) они не влияют.

Диаграмма  полной кинетической энергии механизма Т в функции полного приведенного момента инерции J_п  отличается от диаграммы только положением начала координат . При этом точка  должна быть смещена относительно точки O вниз на расстояние, соответствующее , и влево на расстояние, соответствующее . Получили новую систему координат [T, J_п] с новым началом координат .

Замкнутая кривая  относительно этой новой системы будет диаграммой энергомасс, построенной для установившегося режима. Соединим любую точку кривой энергомасс с началом координат и отметим угол ψ.

Из рис. 6.6 следует, что произвольной точке диаграммы энергомасс соответствует определенный угол наклона прямой, проведенной из начала координат в эту точку

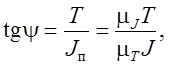                                                  (6.18)

где  – масштабные коэффициенты моментов инерции и кинетических энергий, кг·м²/мм, Н·м/мм.

Так как 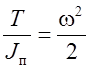, то можно записать  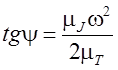или 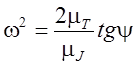, т.е. каждому углу наклона прямой, соединяющей произвольную точку диаграммы с началом координат, соответствует определенная угловая скорость звена приведения или каждому значению угловой скорости звена приведения соответствует определенный угол наклона прямой, проведенной из начала координат через соответствующую точку диаграммы.

Максимальному и минимальному углам наклона касательных соответствует максимальная и минимальная угловые скорости звена приведения:

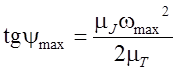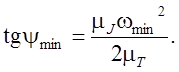;                             (6.19)

Такие скорости возникают в механизме без маховика. Коэффициент неравномерности в этом случае не равен заданному.

Можно найти угловые скорости ω_max  и ω_min через заданный коэффициент неравномерности δ (6.3) и определить соответствующие углы наклона касательных к диаграмме энергомасс.

Получим

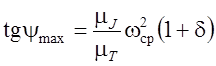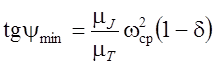; .              (6.20)

Пусть диаграмма ΔТ(Δ J_п) построена. Поскольку величины T₀ и J_м неизвестны, то осей J_п и T провести нельзя. Чтобы определить их положение, пользуясь формулами (6.20) подсчитываем по заданным величинам ω_ср и δ значения ψ_max и ψ_min, а затем под этими углами проводим лучи, касательные к замкнутой кривой ΔТ(Δ J). В точке их пересечения находится начало координат . Определив его и измерив отрезок , подсчитаем искомый момент инерции маховика

                                      (6.21)

Величины углов ψ_max и ψ_min весьма близки друг к другу, поэтому точка их пересечения (начало координат) получается столь удаленной от диаграммы ΔТ(Δ J_п), что не помещается в пределах чертежа. В связи с этим момент инерции J_м нужно находить не по отрезку , а по отрезку , отсекаемому лучами на оси ΔТ. Из рис. 6.6, б