Динамический анализ и синтез механизмов, страница 9

i	, Н	, мм	,  Н	, мм	, Н	, мм	, Н	, мм	, Нм
0	2500		147,15		196,2		98,1
1	2500		147,15		196,2		98,1
2	2500	- 44	147,15	6	196,2	10	98,1	-6	-260,939
3-7	–	–	–	–	–	–	–	–	–
8	0	-32	147,15	3	196,2	-2	98,1	3	1,294
9-12	–	–	–	–	–	–	–	–	–

По данным табл. 6.1 строится диаграмма приведенного момента сопротивления. Примем масштаб оси ординат

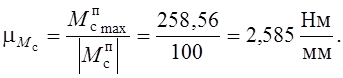
Масштаб оси абсцисс μ_j

, где l – отрезок оси абсцисс, соответствующий одному циклу движения механизма, мм.

6.3.5. Построение диаграммы работ сил сопротивления и движущих сил

Путем графического интегрирования диаграммы приведенного момента сопротивлений строится диаграмма работ сил сопротивления  (рис. 6.13).

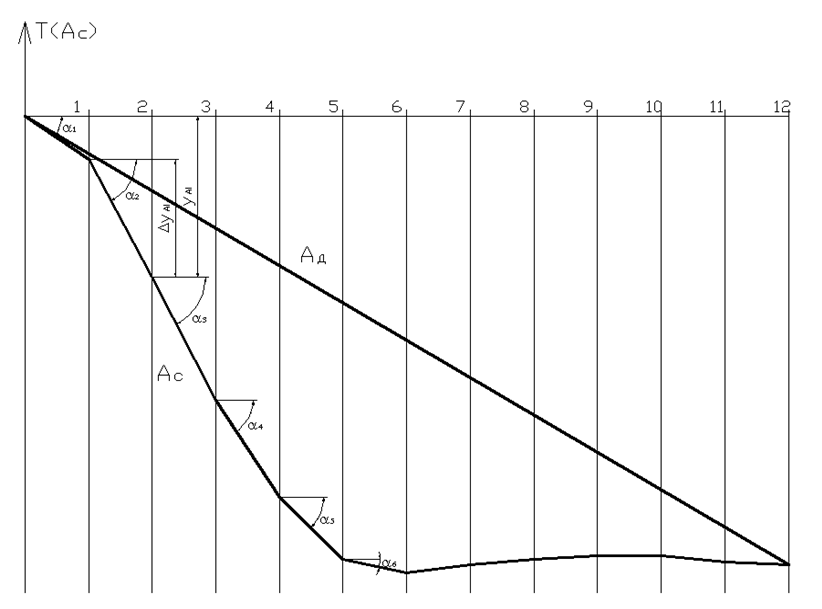
Рис. 6.13. Диаграмма работ сил сопротивления и движущих сил, μ_T(A)=3,386 Нм/мм

При графическом интегрировании график подынтегральной функции вычерчивается в масштабе по осям координат. В рассматриваемом случае это будет  – масштаб приведенного момента сил сопротивления, Н·м/мм;  – масштаб угла поворота звена приведения, рад/мм. Следовательно, ордината  и абсцисса , измеряемые на графике в мм, связаны с физическими величинами следующими соотношениями:

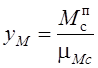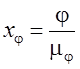, , где .

Угол поворота  делится на 12 равных интервалов , при этом 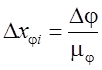, где .

В пределах каждого интервала  подынтегральную функцию определяют с помощью равновеликого по площади прямоугольника, заменяющего на данном интервале криволинейную трапецию. Среднее значение ординаты  на данном интервале соответствует среднему значению суммарного приведенного момента : 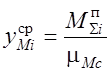, где . Выравнивание площадей прямоугольника и криволинейной трапеции соответствует соотношению

.

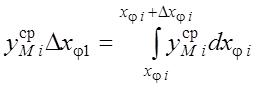Отрезки  проецируются на ось ординат, и полученные точки соединяются с началом отрезка H интегрирования, конец которого совмещен с началом координат заданного графика. Длина отрезка H определяет масштаб графика и выбирается с учетом формата для построений.

На рис. 6.12 длина отрезка H принята 50 мм.

.

Такое построение образует ряд лучей, выходящих из начала O отрезка интегрирования и наклоненных под углами  к положительному направлению оси абсцисс. Эти углы могут быть положительными и отрицательными.

Для произвольного выбранного луча 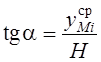. Для первого интервала (от позиции 0 до 1) 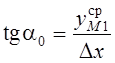. Для построения искомого  графика интегральной зависимости выбирают начало координат  (рис. 6.13), j и проводят последовательно лучи под углами , каждый из которых соответствует определенному интервалу j₁ – для 1–2, j_i – для i…(i+1).

Принятое построение соответствует соотношениям

; .

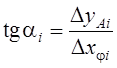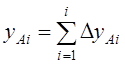Так как углы наклона лучей одинаковы, то записывается равенство правых частей 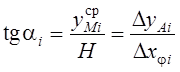. После подстановки получают

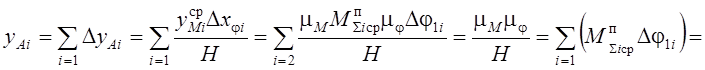
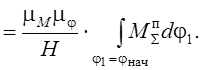
Следовательно, принятая система построений обеспечила получение отрезка , пропорционального значению интеграла в заданных пределах изменения угла j₁. При этом построении имеет место определенная зависимость между масштабами 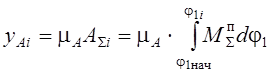, где , .

После нахождения отдельных значений искомой функции в конце интервалов, полученные точки аппроксимируют плавной кривой. При нулевых значениях подынтегральной функции искомая функция имеет максимальные или минимальные значения.

Диаграмма работы движущих сил  для рабочих машин, с учетом принятых выше допущений, получается в виде прямой линии, соединяющей начало и конец графика работы, построенного ранее. Графически дифференцируя полученную линейную зависимость, находим в системе координат .