Динамический анализ и синтез механизмов, страница 5

,

Подставляя в это равенство из формул (6.20) значения tgψ_max и tgψ_min и пользуясь формулой (6.21), определяем величину J_м приведенного момента инерции маховика        

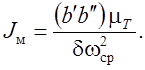                                             (6.22)

Таким образом, для подсчета J_м не нужно искать начало координат и отрезок , достаточно определить отрезок . Отрезок представляет собой наибольший перепад кинетической энергии маховика в масштабе μ_Т  . Выражение (6.22) примет вид

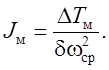                                             (6.23)

Изложенное позволяет заключить, что положение оси J_п никак не влияет на величину момента инерции маховика J_м, поэтому начальное значение кинетической энергии Т₀ вычислять не требуется. То есть начало диаграммы энергомасс ΔТ(ΔJ_п) совпадает с началом координат в точке О.

6.2.2. Способ Н. И. Мерцалова и К. Э. Рериха

Способ Н. И. Мерцалова и К. Э. Рериха основан на определении кинетической энергии всех звеньев механизма и последующем выделении из этой кинетической энергии той ее части, которая приходится только на звено приведения и на звенья, связанные с ним постоянным передаточным числом. После этого легко определить искомое значение наибольшего перепада кинетической энергии ΔТ_{1 наиб}.

Составим выражение кинетической энергии для всего механизма:

.

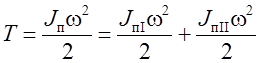Обозначим

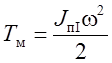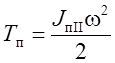, ,                                    (6.24)

где Т – кинетическая энергия всех звеньев механизма; Т_м – кинетическая энергия звеньев механизма, имеющих постоянный приведенный момент инерции (звено приведения и звенья, связанные с ним постоянным передаточным отношением); Т_п – кинетическая энергия тех звеньев механизма, приведенный момент инерции которых переменен.

Из уравнения (6.24)

                                             (6.25)

Кинетическую энергию Т выразим из уравнения

,                                         (6.26)

тогда

.                                   (6.27)

По уравнению (6.27) для одного полного цикла построим диаграмму Т_м(j), где j – угол поворота звена приведения, и по этой диаграмме найдем величину ΔТ_{1 наиб}, входящую в расчетную формулу (6.11).

Проиллюстрируем сказанное графиками. Пусть известны диаграмма (верхняя кривая рис. 6.7, а), построенная относительно оси j, и диаграмма Т_п(j) (рис. 6.7, б).

Согласно уравнению (6.27) прибавим к сумме работ  значение кинетической энергии Т_нач всего механизма в начале цикла. Так как Т_нач является постоянной величиной, то прибавление ее, сделанное графически, представится перемещением оси j на величину Т_нач (рис. 6.7, а). После указанного перемещения верхняя кривая на рис. 6.7, а будет относительно сдвинутой оси  изображать кинетическую энергию Т всего механизма, как это следует из уравнения (6.26). Вычтем, согласно уравнению (6.25), из кинетической энергии всего механизма Т кинетическую энергию Т_п, получим нижнюю кривую на рис. 6.7, а. Нижняя кривая, отнесенная к сдвинутой оси  и явится кривой кинетической энергии Т_м. Отметим на этой кривой точку максимума и точку минимума ,  и по ним определим наибольший перепад кинетической энергии ΔТ_{1 наиб}, необходимый для подсчета  J_п1 по (6.11).

Искомая величина ΔТ_{1 наиб} зависит только от конфигурации кривой Т_м. Форма же кривой Т_м определяется исключительно очертаниями графиков и Т_п(j) и не зависит от значения Т_нач. Любое изменение величины Т_нач изменяет лишь расстояние между осями j и , но форма кривой Т_м, а потому и  значение ΔТ_{1 наиб} при заданных очертаниях кривых и Т_п(j) останутся без изменения. Отсюда следует, что для определения наибольшего перепада кинетической энергии ΔТ_{1 наиб} не нужно знать величины Т_нач, т. е. нет необходимости численно выявлять положения сдвинутой оси абсцисс .

6.2.3. Способ Е. М. Гутьяра

Составим две новые функции и  в соответствии с уравнениями

,                                       (6.28)

,                                       (6.29)