Динамический анализ и синтез механизмов, страница 6

где Т₀ – кинетическая энергия машины в начальном положении; ΔТ – приращение кинетической энергии машины, соответствующее повороту главного вала из начального положения в положение, определяемое углом j; 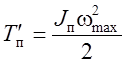,  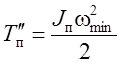– максимальная и минимальная кинетическая энергия всех звеньев машины (без маховика).

Сравнивая уравнения (6.28) и (6.29) с уравнением (6.14), заключаем, что функция Т_м имеет одно и то же наибольшее значение с функцией (в положении, когда ω = ω_max) и одно и то же наименьшее значение с функцией (в положении, когда ω = ω_min).

На основании сказанного имеем

,                                            (6.30)

.                                        (6.31)

Применим уравнения (6.28) и (6.29) к начальному положению машины

,                                        (6.32)

.                                        (6.33)

Вычитая (6.32) и (6.33) соответственно из (6.28) и (6.29), получим

,                           (6.34)

.                         (6.35)

Обозначим

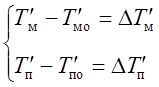   ,                                     (6.36)

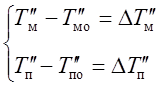   .                                    (6.37)

Подставляя (6.36) в (6.34) и (6.37) в (6.35), получим

,                                         (6.38)

.                                        (6.39)

Напишем формулы для подсчета величин  и

,                        (6.40)

.                        (6.41)

Пользуясь уравнениями (6.40) и (6.41) подсчитываем ряд значений величин  и  и строим диаграммы  и  (рис. 6.8, б).

Вычитая соответственно ординаты этих диаграмм из ординат диаграммы  (рис. 6.8, а, кривая α ), получаем диаграммы  и  (кривые c, d). На основании этих диаграмм получаем

,                                         (6.42)

.                                         (6.43)

Вычитая (6.43) из (6.42), получаем

.                    (6.44)

Диаграммы  ,  и  строятся в одних и тех же масштабах  и . Получим другое выражение левой части уравнения (6.44). Для этого используем равенства

,

                                                                                                                     (6.45)

.

Вычитая равенства (6.45) одно из другого, получим

.              (6.46)

На основании (6.30) и (6.31) имеем

.                 (6.47)

Вычитая равенство (6.32) из (6.33), получим

.                     (6.48)

Подставляя (6.47) и (6.48) в (6.46), получим

.               (6.49)

Подставляя формулу  в (6.49), имеем

.                         (6.50)

Сравнивая уравнения (6.44) и (6.50), получим

.

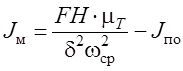6.3. Пример расчета махового колеса

На листе проекта отражаются результаты работы по проведению динамического анализа и синтеза машины, т.е. определения параметров динамической модели и закона движения начального звена механизма.

Результаты выполнения всех этапов должны найти отражение в пояснительной записке и на листе проекта формата  A1.

Работу рекомендуется выполнять в такой последовательности.

6.3.1. Анализ исходных данных

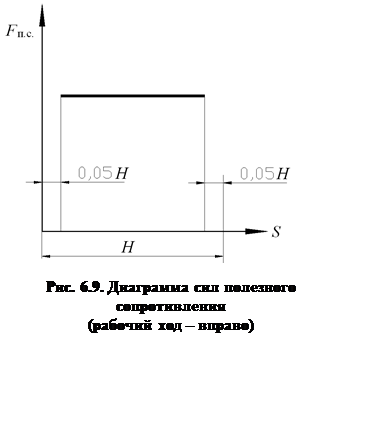
Ознакомиться с заданием и числовыми значениями исходных данных. Отразить их в пояснительной записке.

Исходные данные представлены на рис. 6.9.

,

,

,

,

,

,

,

,

,

,

.

Масса (кг) i-го звена с постоянным поперечным сечением определяется по формуле

,                                              (6.51)

где m_l – масса единицы длины звена (линейная плотность ρ_l), кг/м; l_i – длина звена, м.

6.3.2. Вычерчивание схемы механизма в масштабе длин

Строим план механизма в 12 положениях рис. 6.10.

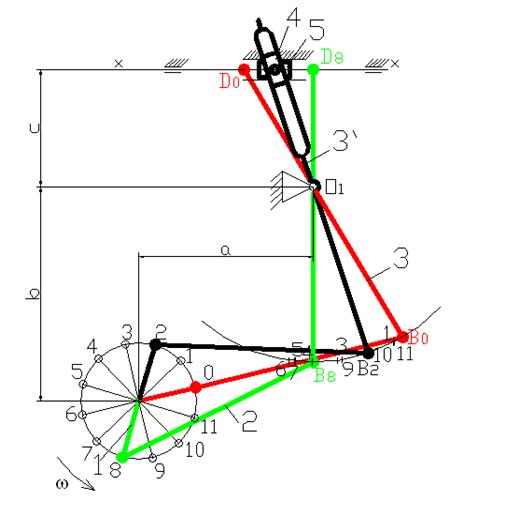
Рис. 6.10. План механизма, μ_l = 0,008 м/мм

Определяем масштабный коэффициент длин

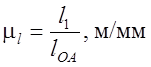,                                               (6.52)

где l₁ – истинная длина звена (кривошипа OA), м;  – выбранный чертежный размер звена (кривошипа), мм.

.

В соответствии с формулой 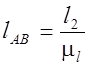 (где  – чертежная длина звена, например, AB, мм, l₂ – истинный размер звена, м) находим чертежные и координатные размеры всех остальных звеньев механизма:

, , , , , .