Динамический анализ и синтез механизмов, страница 8

Скорость т. D₅ – общей для звеньев 4 и 5, находим, раскладывая движение на переносное (вращательно) вместе с т. D₃ и относительное (поступательное) по отношению к точке D₃. В абсолютном движении точка D₅ перемещается вдоль оси x–x.

Поэтому ,

, где – переносная скорость, ее вектор изображен на плане;  – относительная скорость, ее вектор параллелен звену DO₁, так как ползун D₄ относительно кулисы движется параллельно DO₁;  – переносная скорость т. D₀, совпадающей с D, но принадлежащей неподвижной направляющей, следовательно ;  – относительная скорость точки D, лежащей на ползуне и точки D₀, лежащей на неподвижной направляющей, ее вектор параллелен направляющей x–x.

Через точку d₃ проводим линию, параллельную DO₁, а через полюс p – линию, параллельную x–x, до пересечения их в точке D_4,5. Вектор pd_4,5 изображает скорость точки D₅.

6.3.4. Построение диаграммы приведенного момента

сопротивления

Для построения диаграммы приведенного момента сопротивления (рис. 6.12)  используется метод возможных перемещений. Согласно этому принципу, если  в некотором положении механической системы с двусторонними идеальными связями приложенные к ней силы уравновешиваются, то на любом возможном перемещении системы из этого положения сумма работ задаваемых сил равна нулю.

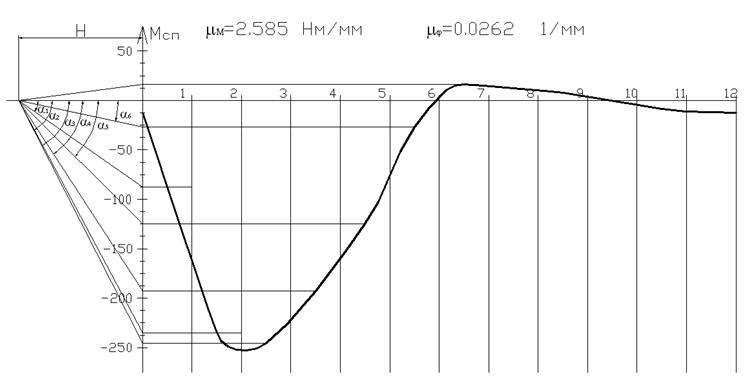
Рис. 6.12. Диаграмма приведенного момента сопротивления,

,

Направления элементарных возможных перемещений точек механизма совпадают с направлениями скоростей этих точек. Если разделить все работы на время, не равное нулю, то получим условие равенства нулю мгновенных мощностей.

По диаграмме сил сопротивления определяются положения механизма,  в которых действует сила F_п.с. На планах скоростей указываются направления активных сил (сил тяжести G) и сил сопротивления F_п.с, инерционные нагрузки не учитываются.

Сила тяжести   приложена в центре масс звена, сила полезного сопротивления действует на выходное звено и направлена противоположно вектору скорости выходного звена. Спроектируем скорости точек приложения сил на направления этих сил. Проекции скоростей обозначим индексами тех сил, на направления которых спроектированы векторы скорости. Например,  означает проекцию скорости V точки приложения силы  на направление этой силы. Полученные мощности подставляем в уравнение.

Для каждого из 12 положений механизма определяется величина приведенного момента сопротивления по формуле

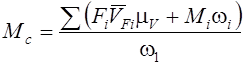,                                     (6.55)

где    – проекции скоростей на направление сил.

К рассматриваемому механизму не приложены моменты сил. Инерционные моменты  будут учтены через приведенный момент инерции . Формула (6.55) примет вид

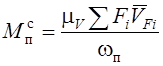,                                         (6.56)

где  – масштаб плана скоростей, м/с·мм;  – силы, приложенные к механизму, Н;  – проекция скоростей центра масс звена на направление силы, мм;  – угловая скорость звена приведения, с^-1.

Вычислим силы тяжести. Равнодействующие этих сил приложены в центрах масс звеньев, а величины равны:

.

Сила действует на рабочем ходу ползуна. Рабочий ход ползуна отсчитывается вправо от  положения «0» до положения «5». Знак величин, входящих в формулу, определяется их направлением. Если направление силы совпадает с направлением скорости точки приложения силы, то берется знак «плюс», иначе «минус».

Вычислим приведенный момент сопротивления на холостом ходу. В восьмом положении сила полезного сопротивления не действует, .

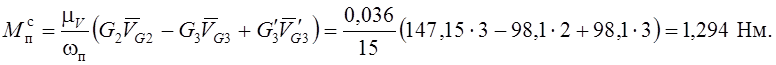
Вычислим приведенный момент инерции на рабочем ходу. Во втором положении действует сила полезного сопротивления .

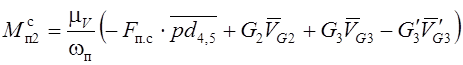, где  – сила полезного сопротивления, Н;  – вектор скорости точки, мм;  – силы тяжести 2, 3, 3’ звеньев, Н;  – угловая скорость звена приведения, с^-1;  – проекции скорости центра масс звена на направление силы, мм.

Сила тяжести кулисы находится на расстоянии  длины от точки крепления (стойка, т. О₁).

Значения моментов сопротивления для других положений механизма и данные для их вычисления приведены в табл. 6.1.

Таблица 6.1

Результаты определения приведенного момента сопротивления