Динамический анализ и синтез механизмов, страница 2

Удобно выразить угловые и линейные скорости через длины векторов планов скоростей. Если приведение выполняется к ведущему звену OA, тогда: , , 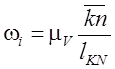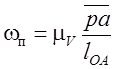. Здесь – длина вектора скорости центра масс i-го звена, мм; – угловая скорость i-го звена, с^-1;  – длина вектора относительной скорости точек K и N, мм;  – длина звена KN, мм;  – длина вектора скорости звена точки А, мм;  – истинная длина звена ОА, мм;  – масштаб плана скоростей, м/с·мм.

Теперь выражение для приведенного момента инерции можно записать следующим образом:

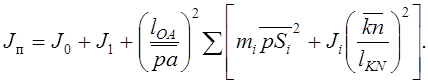                     (6.2)

Вычислив  для ряда последовательных положений механизма за один цикл его движения, полученные данные заносим в таблицу и по ним строим функции . Начало координат графика размещаем в начале рабочего хода машины (рис. 6.3).

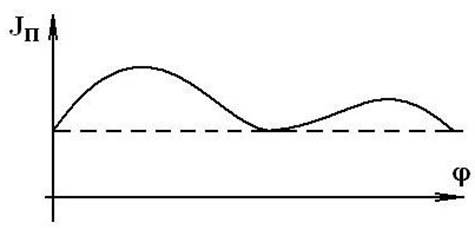
Рис. 6.3. Диаграмма приведенного момента инерции

Приведенный к главному валу момент инерции машины равен сумме приведенных к главному валу моментов инерции всех звеньев машины  и момента инерции маховика :

                                             (6.3)

Приведенные моменты инерции  и  являются периодическими функциями положения машины.

6.1.3. Приведенный момент сил

Приведение сил и моментов сил, действующих на механизм, осуществляется также при условии эквивалентности динамической модели и механизма (равенства их элементарных работ).

Приведенный момент сил  – это пара сил, приложенная к звену приведения и определяемая из равенства элементарной работы этой пары сил сумме элементарных работ сил и моментов пар сил, действующих на звенья механизма. Из равенства элементарных работ вытекает равенство мгновенных мощностей

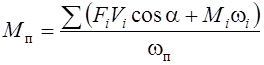,                                      (6.4)

где   – приведенный момент, приложенный к звену приведения, Н·м;  – сила, приложенная к i-й точке, Н;  – скорость i-й точки, м/с;  – угол между направлениями силы и скорости ;  – момент, приложенный к i-му звену, Н·м;  – угловая скорость звена приведения, рад/с.

Для механизма, рассматриваемого в курсовом проекте, внешними силами являются: силы тяжести звеньев ; сила полезного сопротивления; действующая на рабочем ходу; момент сил сопротивления  (принимают постоянным).  Силы  инерции  и  моменты  сил инерции   звеньев  не  учитываются,  так  как  рассматривается  безмассовый  скелет  механизма  со  всеми приложенными к нему нагрузками. Массы звеньев учитываются при определении приведенного момента инерции .

Приведенным моментом  может быть как момент сил сопротивления , так и движущий момент . Для машин-двигателей определяется приведенный движущий момент , а момент сопротивления  принимается постоянным. Для рабочих машин определяется приведенный момент сопротивления  по формуле (6.4), а движущий момент принимается постоянным . В курсовом проекте рассматривается рабочая машина.

Приведенные моменты  вычисляют, используя метод возможных перемещений. Вычислив  для ряда последовательных положений механизма за один цикл его движения, заносят полученные данные в таблицу и по ним строят график  (рис. 6.4). Суммарный приведенный момент заменяет собой все силы и моменты.

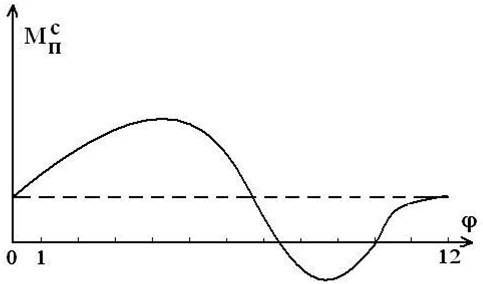
Рис. 6.4. Диаграмма приведенного момента

6.1.4. Кинетическая энергия

Построив динамическую модель исследуемого механизма (рис. 6.2), приступим к её анализу. На основании определения приведенного момента инерции получаем формулы.

Кинетическая энергия всей машины, включая маховик,

.                                          (6.5)

Кинетическая энергия маховика

.                                          (6.6)

Кинетическая энергия всех звеньев машины без маховика

.                                                   (6.7)

Очевидно,

.                                                  (6.8)

Так как ω, J и J_п – величины переменные, то в уравнениях (6.5) и (6.7) Т и Т_п  являются функциями двух переменных величин. В отличие от этого, Т_м является функцией одной переменной величины, угловой скорости ω, так как J_м – величина постоянная.

Кинетическая энергия звена приведения

                                                 (6.9)

откуда может быть найдена скорость звена приведения ω_п