расстояние между нижними точками провеса провода и троса;
[fПР] - допустимая стрела провеса провода;
[fТР] - допустимая стрела провеса троса.
[fПР] = h1-l-Г-Dh =19-1,3-6-0,2=11,5 м.
Для опор башенного типа средняя высота подвеса проводов:
![]() м
м
Высота приведенного центра тяжести провода:
hПР=hСР- 2/3[fПР]=19,7 - 7,6 = 12,1 м.
Исходные данные:
Сталеалюминевый провод АС185/43 для воздушных линий 110 кВ, ветровой район - III, район по гололеду - I.
Провод АС 185/43: общее сечение 185мм2; диаметр 19,6 мм., масса одного километра 846 кг.
Внешние нагрузки на ЛЭП можно разделить на следующие виды:
1. Собственный вес - вертикальная нагрузка.
2. Ветровая нагрузка - горизонтальная
3. Гололедная нагрузка - вертикальная
4. Комбинация перечисленных нагрузок
Погонная (единичная) нагрузка - нагрузка на 1 метр длины.
Обозначение: Pi : [![]() ]
]
Удельная нагрузка - единичная нагрузка, приведенная на 1 мм2 сечения.
Обозначение: gi : [![]() ]
]
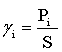 ,
где S - площадь фактического
сечения провода.
,
где S - площадь фактического
сечения провода.

P1 : g1
Рис. 4.1. Сила веса
Провод: 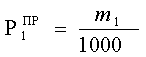 =
= ![]() =
0,846
=
0,846 ![]() .
.
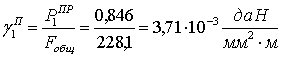 .
.
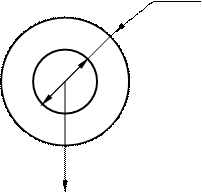 Cмах
Cмах
d
P2
Рис. 4.2. Вес гололеда
P2=0.9pCmax(d+Cmax)*10-3
d - диаметр провода
Смах - максимальная толщина стенки гололеда.
Нормативная толщина стенки гололеда (в мм) для высоты 10 м. над поверхностью моря.
Таблица 4.1.
|
Район по гололеду |
Повторяемость |
|
|
1 раз в 5 лет |
1 раз в 10 лет |
|
|
I |
5 |
5 |
|
II |
5 |
10 |
|
III |
10 |
15 |
|
IV |
15 |
20 |
|
Особый |
20 и более |
более 22 |
Cmax=5;
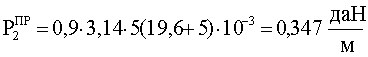 .
.

Р1
Р2
Р3
Рис. 4.3. Провод с гололедом
![]()
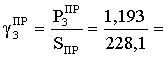 5,2*10-3
5,2*10-3
![]()

Р4
Рис. 4.4. Ветровая нагрузка
![]()
Где: q - скоростной напор ветра
Ветровая нагрузка ![]() ,
V - скорость ветра
,
V - скорость ветра
Нормативные скоростные напоры и скорости ветра для высоты до 15 м. над землей
Таблица 4.2.
|
Ветровой район |
Повторяемость |
|||||
|
1 раз в 5 лет |
1 раз в 10 лет |
1 раз в 15 лет |
||||
|
q |
V |
Q |
V |
Q |
V |
|
|
I |
27 |
21 |
40 |
25 |
55 |
30 |
|
II |
35 |
24 |
40 |
25 |
55 |
30 |
|
III |
45 |
27 |
50 |
29 |
55 |
30 |
|
IV |
55 |
30 |
65 |
32 |
80 |
36 |
|
V |
70 |
30 |
80 |
36 |
80 |
36 |
Для III ветрового района: q = 50 ![]()
V = 29 ![]()
 F - площадь метрового сечения
метрового отрезка провода в мм2
F - площадь метрового сечения
метрового отрезка провода в мм2
Рис. 4.5. Продольное сечение 1 метра провода без гололеда
F = d*10-3 м2
F ПР = 19,6*10-3 м2
j - угол между направлением ветра и проводом (тросом)
j=90 0 => sinj = 1
CX - аэродинамический коэффициент (коэффициент любого сопротивления), зависит от скорости ветра, плотности воздуха, формы, протяженности и шероховатости обдуваемой поверхности. Согласно ПУЭ Сх = 1,1 - для проводов и тросов более 20 мм., для проводов и тросов диаметром менее 20 мм. Сх = 1,2, а также для проводов и тросов любого диаметра, покрытых гололедом.
a(q) - коэффициент, учитывающий неравномерность скоростного напора ветра.
Таблица 4.3. Значение a(q)
|
q, дан/мм2 |
До 27 |
40 |
55 |
76 и более |
|
a(q) |
1 |
0,85 |
0,75 |
0,7 |
КН - коэффициент, учитывающий увеличение скоростного напора ветра по высоте (зависит от высоты приведенного центра тяжести провода)
Таблица 4.4. Зависимость КН от hЦТприв
|
hЦТприв |
До 15 |
20 |
30 |
40 |
60 |
100 |
200 |
300 и более |
|
Кh |
1,0 |
1,25 |
1,4 |
1,55 |
1,75 |
2,1 |
2,6 |
3,1 |
Kh=1;
Промежуточные значения определяются методами линейной интерполяции.
KL - коэффициент, зависящий от длины габаритного пролета.
Таблица 4.4. Зависимость КL от lгаб
|
lгаб |
0 |
100 |
150 |
250 и более |
|
KL |
1,2 |
1,1 |
1,05 |
1 |
KL =1;
![]()
 |
|||
 |
|||
Cmax
d
Рис. 4.6. Продольное сечение 1 метра провода с гололеда
q5 = 0.25q = 12,5 ![]()
где q - нормативный скоростной напор ветра.
a5 = a(0,25q) = 1; Cx* = 1,2;
Fпр* = (d+2 Cmax)*10-3 = (19,6 + 2*5) =29,6*10-3
P5пр = a5KLKHCX*0.25q*Fпр = 1*1*1,2*12,5*29,6*10-3 = 0,444 ![]()
 |
Рис. 4.7. Нагрузка без гололеда
Р6=![]() =
1,264
=
1,264 ![]()
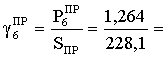 5,54*10-3
5,54*10-3
![]()
 |


 Р5
Р5
Р3 Р7
Рис. 4.8. Результирующая нагрузка
Р7 =![]() =
1,272
=
1,272 ![]()
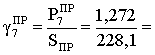 5,57*10-3
5,57*10-3 ![]()
Таблица 4.6. Единичные и удельные нагрузки на провод.
|
Нагрузка |
Провод |
|
|
Pi, |
gi, |
|
|
P1, g1 |
0,846 |
0,0037 |
|
P2 |
0,347 |
- |
|
P3, g3 |
1,193 |
0,0052 |
|
P4 |
0,94 |
- |
|
P5 |
0,444 |
- |
|
P6, g6 |
1,264 |
0,00554 |
|
P7, g7 |
1,272 |
0,00557 |
Вывод: наибольшей нагрузкой на провод и трос является нагрузка P7, g7 , то есть при ветре и гололеде.
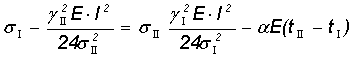
Параметры:
gI sI tI – исходный режим
gII sII tII – состояние и климатический режим в котором находится провод.
l - расстояние между опорами,
Е - модуль упругости.
a-температурный коэффициент расширения.
Определение 1: Критическим пролетом называется пролет (L), вычисленный из уравнения состояния провода при заданных исходных и конечных параметрах.
( gI sI tI gII sII tII)
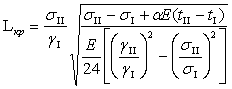
Определение 2: Первым критическим пролетом называется пролет такой длины, при котором напряжение проводе в режиме среднегодовой температуры равно допускаемому напряжению в том же режиме (sII=[stэ]), а в режиме наименьшей, температуры равно допускаемому напряжению при наименьшей температуре.
[sI]= [stmin]
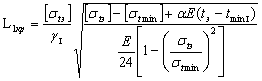
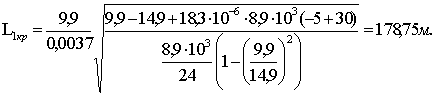
Определение 3: Вторым критическим пролетом называется пролет такой длины, при котором напряжение в проводе в режиме максимальных нагрузок и низких температур равно своим допускаемым напряжениям в этих режимах.
[sII]=[smax] sI=[st min]
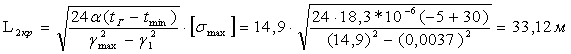
Определение 4: Третьим критическим пролетом называется пролет такой длины, при которой напряжение в проводе в режиме максимальной нагрузки и среднегодовой температуры равно своим допустимым напряжениям.
[sII]=[stэ] sI=[smax]
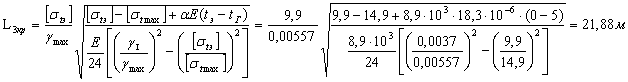
Таблица 5.1.
|
Случай |
Соотношение |
Исходное напряжение |
Расчетный критический пролет |
|
1 |
L 1кр< L 2кр< L 3кр |
[stmin] ; [smax] ; [stэ] |
L1кр ; L 2кр |
|
2 |
L 1кр> L 2кр> L 3кр |
[stmin] ; [smax] |
L 2кр |
|
3 |
L 1кр – мнимый L 2кр< L 3кр |
[smax] ; [stэ] |
L3кр |
|
4 |
L3кр – мнимый L1кр<l2кр |
[stmin] ; [stэ] |
L1кр |
Вывод: выполняется условие L 1кр > L 2кр > L 3кр, следовательно, L 2кр - расчетный пролет
[stmin]; [smax]; [stэ] - исходные напряжения.
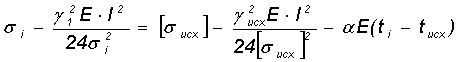
gисх, sисх, tисх выбираем из таблицы 6.1. => [sисх]=[smax]=14,9 ![]()
gисх=gmax=g7=0,00557![]() ; tисх=tГ=-50C.
; tисх=tГ=-50C.
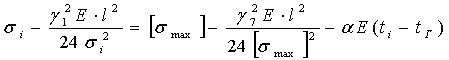
Рассчитаем по уравнению состояние провода si затем по формуле 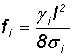 найдем
стрелы провеса провода.
найдем
стрелы провеса провода.
Таблица 6.1. Расчетные режимы провода
|
Расчетный режим, i |
Сочетание климатических условий |
Номер нагрузки, даН/мм2м |
|
I |
Провод и трос покрыты гололедом, скоростной напор ветра 0,25q tI=tГ =-5 0 |
g7 =0,00557 |
|
II |
Провод покрыт гололедом, ветра нет tII=tГ =-5 0 |
gII=g3 =0,0052 |
|
III |
Скоростной напор ветра равен q, гололеда нет tIII=tГ =-5 0 |
gIII=g6 =0,00554 |
|
IV |
Среднегодовая температура, ветра и гололеда нет. TIV=tЭ =-5 0 |
gIV=g1 =0,0037 |
|
V |
Ветра и гололеда нет tV=15 0 |
gV=g1 =0,0037 |
|
VI |
Ветра и гололеда нет tVI=tmin = -30 0 |
gVI=g1 =0,0037 |
|
VII |
Ветра и гололеда нет tVI=tmax = +40 0 |
gVII=g1 =0,0037 |
Расчет режимов:
![]()
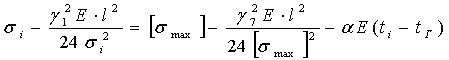 ;
; 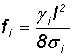
I.![]()
si =14.9 ![]()
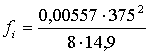 =6,57м
II.
=6,57м
II. 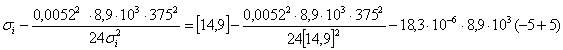 si = 13,86
si = 13,86 ![]()
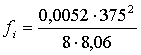 =11,3м
=11,3м
III.
![]() si = 8,05
si = 8,05 ![]()
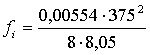 =12,09м
=12,09м
IV.![]() si = 11,68
si = 11,68 ![]()
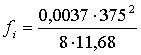 =5,56м
=5,56м
V.
![]() si = 8,42
si = 8,42 ![]()
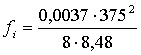 =7,66м
=7,66м
VI.
![]() si = 7,63
si = 7,63 ![]()
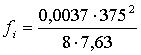 =8,51м
=8,51м
VII.
![]() si = 4,35
si = 4,35 ![]()
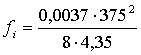 =14,95м
=14,95м
Результаты расчетов сведем в таблицу
Таблица 6.2. Напряжения и стрелы провеса в расчетных режимах
|
№ pежима |
sI |
smax |
fi, м |
[fпр], м |
|
I |
14,9 |
14,9 |
6,57 |
11,5 |
|
II |
13,86 |
11,3 |
||
|
III |
8,05 |
12,07 |
||
|
IV |
11,86 |
5,56 |
||
|
V |
8,42 |
8,42 |
||
|
VI |
7,63 |
8,51 |
||
|
VII |
4,35 |
14,95 |
Выводы:
1. Для всех режимов условия прочности провода выполняются.
2. Условия жесткости не выполняются во всех режимах.
Критической температурой называется такая температура, при которой стрела провеса провода под действием собственного веса равна стреле провеса при наличие гололеда.
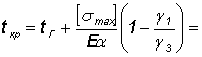
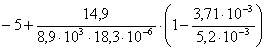 =24,960C
=24,960C
t max=+400C;
Разбивочный шаблон представляет собой 3 квадратичные параболы. С его помощью производится расстановка опор по профилю трассы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
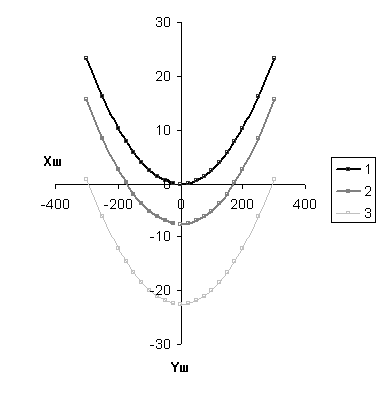
Рис. 7.1. Параболы
1 - кривая провисания, строится по уравнению 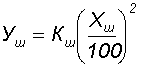
где Кш - масштабный коэффициент шаблона; 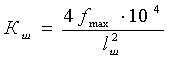
где fmax = 14,95
максимальная стрела провеса провода, lш = lгаб = 375 метров
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.