Измерительные приборы в электрических измерениях, страница 8

Датчики усилий

С целью измерения механической силы упругое тело может быть подвергнуто действию этой силы. Возникающие при этом деформация или изменение размеров данного тела можно измерить затем с помощью датчика смещения. Материал и форму упругого тела в таком «динамометре2 следует выбрать так, чтобы в широком диапазоне удовлетворялся закон Гука без остаточной деформации. Для цилиндрического стержня закон Гука дает:

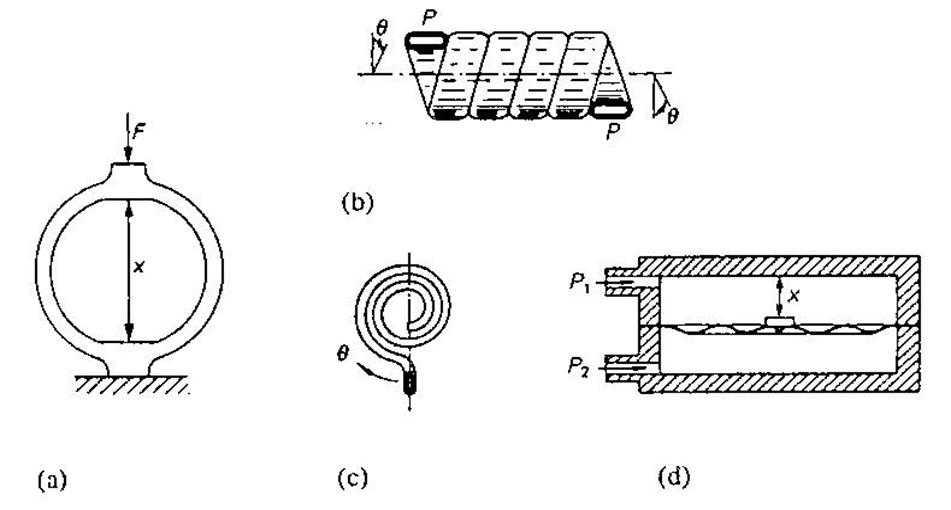
Рис. 3.12. Несколько различных упругих пружинных конструкций для преобразования силы F или давления Р в линейное смещение х или угол поворота q: (а) пружина кольцевого типа; (b) винтовая пружина Бурдона; (с) спиральная пружина Бурдона; (d) мембранная пружина.

.

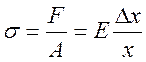Здесь σ – давление на стержень, F – сила, действующая на стержень, А – площадь поперечного сечения стержня и Δх/х – относительное удлинение

(или деформация) стержня. Е – осительное удлинение (или деформация) стержня. На рис. 3.12(b) и (с) показаны действующие по этому принципу, так называемые манометры Бурдона (Bourdon). Величина смещения х или угол поворота θ в этих манометрах обычно измеряются посредством тензорезисторов или дифференциальных трансформаторов смещения.

Пьезоэлектрические датчики силы

У некоторых материалов наблюдается эффект электрической поляризации, изменяющейся при любой механической деформации материала. Когда к небольшому образцу такого материала приложена сила (или на него оказывается давление), между противоположными гранями образца возникает разность электрических зарядов. Это явление называется пьезоэлектрическим эффектом (от греч. piezein – нажать).

Этот эффект наблюдается у материалов, в кристаллической решетке которых отсутствует центр симметрии, например у кварца. Любая внешняя механическая деформация вызывает изменение дипольного момента кристалла. В асимметричном кристалле это изменение различно по разным направлениям, что является причиной макроскопической электрической поляризации, приводящей в результате к возникновению разности зарядов на гранях кристалла. Этот эффект может наблюдаться в материалах, обладающих центром симметрии, если только симметрия нарушена сильным электрическим полем из-за спонтанной поляризации материала. Примером такого класса материалов (так называемых ферроэлектриков) является титанат бария.

Может также наблюдаться обратный эффект: образец пьезоэлектрического материала деформируется, когда к нему приложено электрическое напряжение.

На рис. 3.13(а) показано, как можно воспользоваться пьезоэлектрическим эффектом в датчике давления. Заряд Q, возникающий на гранях кристалла, пропорционален приложенной силе F, а давление Р = АF, где А – площадь поверхности, на которую действует сила F. Чувствительность по заряду S_q пьезоэлектрического датчика силы определяется как

.

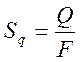Эта чувствительность зависит от материала кристалла и его ориентации, но не зависит от размеров кристалла. Чувствительность по напряжению S_v по определению, равна

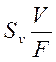
и, поскольку для конденсатора справедливо равенство Q = СV, находим

,

где С – электрическая емкость датчика. Очевидно, что чувствительность пьезоэлектрического датчика по напряжению зависит от его размеров.

На рис. 3.13(b) показана электрическая эквивалентная схема такого пьезоэлектрического датчика. Резистор R, включенный между двумя выводами, отражает обычно очень высокое сопротивление утечки. Благодаря этому становится невозможным с помощью датчика такого типа измерять статические силы. Статическая сила вызвала бы появление на выходе постоянного напряжения. Однако из-за утечки заряда через влажную или загрязненную поверхность и конечное объемное сопротивление величина постоянного напряжения быстро падает.

Некоторые типичные характеристики реального пьезоэлектрического датчика давления таковы: материал – кварц; диапазон измерения 0 – 5000

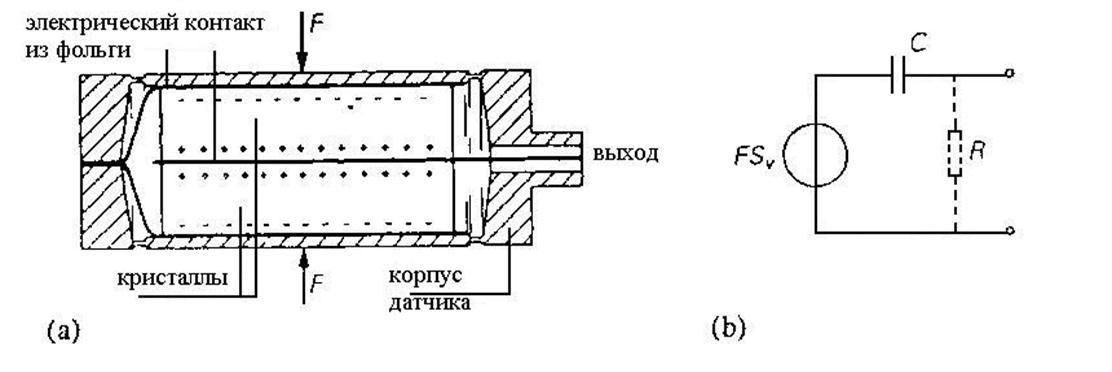
Рис. 3.13. (а) Пьезоэлектрический датчик давления. (b) Эквивалентная электрическая схема.

Н / см²; нелинейность 1%; чувствительность по заряду 3 пКл*см² / Н; температурный коэффициент чувствительности 10^-3 К^-1; емкость 8 пФ; резонансная частота 20 кГц; сопротивление утечки 1012 Ом.

Предположим, что выход пьезоэлектрического датчика соединен со входом усилителя напряжения (усилитель с очень большим входным импедансом). Поскольку усилитель обычно располагается на некотором расстоянии от датчика, соединение осуществляется с помощью длинного кабеля. На рис. 3.14(а), где приведена эквивалентная схема, включающая датчик, кабель и входную цепь усилителя, приняты следующие обозначения: С_c  – емкость, а R_c – сопротивление утечки между двумя проводниками кабеля; С_i – входная емкость, а R_i – входное сопротивление усилителя напряжения. Входное напряжение усилителя равно V_i, поэтому передаточная функция определяется как

.

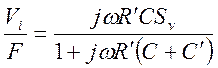В этом выражении  представляет собой параллельное соединение резисторов R, R_c и R_i, а  – параллельное соединение конденсаторов С_c и С_i. На высоких частотах коэффициент передачи становится действительной величиной и равен . Сигнал ослабляется из-за емкости кабеля и входной емкости. Из приведенного выражения для передаточной функции следует, что нижняя граничная частота f₁ по уровню -3 дБ равна . Ниже этой частоты коэффициент передачи уменьшается в 2 раза (на 6 дБ) при понижении частоты на октаву. Поэтому для получения высокой чувствительности и малого значения f₁, входной импеданс усилителя должен быть очень большим. Применяя специальный измерительный усилитель (электрометрический усилитель) можно получить входное сопротивление порядка 10¹⁴ Ом и входную емкость около 1 пФ.

Проблем, связанных с емкостью кабеля и входным импедансом усилителя, можно избежать, применяя в качестве меры силы величину заряда, а не напряжение. Выходной сигнал датчика поступает в этом случае на вход усилителя заряда, схематически изображенного на рис. 3.14(b). Если коэффициент усиления А₀ используемого операционного усилителя очень велик, то входное напряжение будет пренебрежимо малым при конечном