Для измерения среднеквадратических значений шума и сигналов с малым коэффициентом заполнения мы должны знать условия насыщения усилителя S. Хотя среднеквадратическое значение шумового напряжения или импульсного напряжения может быть малым, у них все же могут быть очень большими пиковые значения. Если такие сигналы измеряются электронными измерительными системами, то может случиться так, что в то время, когда усилитель уже находится в насыщении, считываемое (среднеквадратическое) значение все еще мало. В этих измерениях важен так называемый коэффициент амплитуды. Он равен отношению пикового значения сигнала к его среднеквадратическому значению. Обычно для электронных измерителей среднеквадратического значения допустимы сигналы с коэффициент амплитуды вплоть до 10.
3.3.6 Цифро-аналоговое и аналого-цифровое преобразование
Сигнал, величина которого зависит от времени, называется динамическим сигналом. Динамический сигнал можно описать как функцию времени. Если функция определена для всех точек на временной оси (на определенном конечном интервале времени), то мы говорим, что это непрерывный во времени сигнал. Если сигнал, а значит и функция, могут принимать любое значение в пределах некоторого интервала значений, то такой сигнал называют сигналом с непрерывным множеством значений. Почти все сигналы, возникающие в макроскопических физических процессах, являются одновременно и непрерывными во времени и имеющими непрерывное множество значений. Такие непрерывные сигналы, изменяющиеся по мере того, как происходят изменения в (непрерывных) физических процессах, называют аналоговыми сигналами.
Существуют также дискретные во времени сигналы. Значение такого сигнала известно только в определенные дискретные моменты времени и им можно воспользоваться только в эти моменты времени. Дискретный во времени сигнал можно рассматривать как результат взятия выборок непрерывного во времени сигнала (см. параграф 2.2).
Точно так же и величина сигнала может принимать только некоторые дискретные значения. Тогда сигнал называют дискретным по величине сигналом. Такой сигнал может принимать только конечное число значений между заданным верхним и нижним пределами. Процесс преобразования сигнала с непрерывным множеством значений в сигнал с дискретными значениями называется квантованием и реализуется с помощью аналого-цифрового преобразователя. Некоторые из таких преобразователей действуют мгновенно. Тогда непрерывность во времени сохраняется даже для сигналов с дискретными значениями. Однако большинство аналого-цифровых преобразователей действуют не мгновенно, поскольку процедура преобразования требует некоторого времени. Следующее преобразование в последовательности преобразований возможно только тогда, когда выполнено предыдущее. В таких преобразователях должно производиться взятие выборки сигнала, поэтому свойство непрерывности во времени теряется. Сигналы, дискретные по величине и во времени, мы будем называть цифровыми сигналами (от лат. digits – палец).
Прежде чем мы сможем продолжить обсуждение преобразования сигналов, нам следует сначала рассмотреть числовое представление цифрового сигнала, о котором идет речь. Число N представляется набором символов, расположенных в определенном порядке:
![]() .
.
В этом выражении n и m – целые числа. Когда мы выбираем ту или иную форму числового представления, это означает, что
![]() ,
,
где r – основание системы счисления; r – целое число больше единицы. Коэффициенты аi – целые числа, удовлетворяющие условию: 0 ≤ аi ≤ r - 1.
Распространенными представлениями чисел являются системы счисления с основанием 10 (десятичная система), с основанием 8 (восьмеричная система), с основанием 3 (троичная система) и с основанием 2 (двоичная система). Например, в десятичной системе счисления число 701,43 означает 7´102+0´101+1´100+4´10-1+3´10-2. В двоичной системе счисления число 1011,01 = 1´23+0´22+1´21+1´20+0´2-1+1´2-2, которое в десятичной системе счисления равно 11,25.
В десятичной системе (r = 10) коэффициенты ai называются десятичными цифрами, а в двоичной системе (r = 2) – двоичными цифрами или обычно короче: битами. Первый бит аn является старшим значащим разрядом, а последний бит, имеющий наименьшее значение, является младшим значащим разрядом. Обычно цифровой сигнал бывает представлен в виде последовательности двоичных цифр; то есть является двоичным сигналом. В таких сигналах два различных уровня сигнала часто обозначают как «0» и «1». Величина «0» обычно соответствует меньшей величине сигнала, а «1» – большей величине сигнала.
Предпочтение, отдаваемое двоичной системе, является следствием того факта, что многие простые электронные, гидравлические и другие системы имеют два устойчивых состояния, как у выключателя (замкнуто или разомкнуто), реле, триггера, ферритового сердечника памяти (два направления намагничивания). Поэтому в компьютерах также применяют двоичную систему счисления. Для того, чтобы компьютеры могли работать с аналоговыми величинами, эти величины необходимо преобразовать в поток битов с помощью аналого-цифровых преобразователей. Конечно, когда результат вычисления должен быть доступен в аналоговой форме, например, при управлении процессом с помощью аналогового воздействия, например, с помощью тока, требуется и обратная операция.
Наблюдатель, считывающий положение стрелки, помещенной перед шкалой, фактически также выполняет функцию аналого-цифрового преобразователя: аналоговому отклонению стрелки приписывается дискретная величина.
Цифро-аналоговое преобразование
Цифро-аналоговый преобразователь (ЦАП) отображает цифровой сигнал в аналоговый. Ради простоты, мы рассмотрим ниже только аналоговые напряжения. Цифровой сигнал, представленный n + 1 битами параллельно, в некоторый фиксированный момент времени, имеет величину
![]() .
.
Если пока не рассматривать дробные числа и числа со знаком, то цифро-аналоговое преобразование описывается следующим простым соотношением:
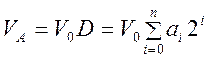 ,
,
где V0 – малое фиксированное приращение напряжения, а Va – аналоговое напряжение на выходе ЦАП. График, характеризующий передаточную характеристику ЦАП, приведен на рис. 3.6l(a). Dможет принимать только конечное число дискретных значений. Минимальный шаг, с которым может увеличиваться VA, равен точно V0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.