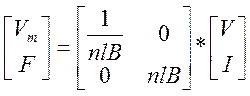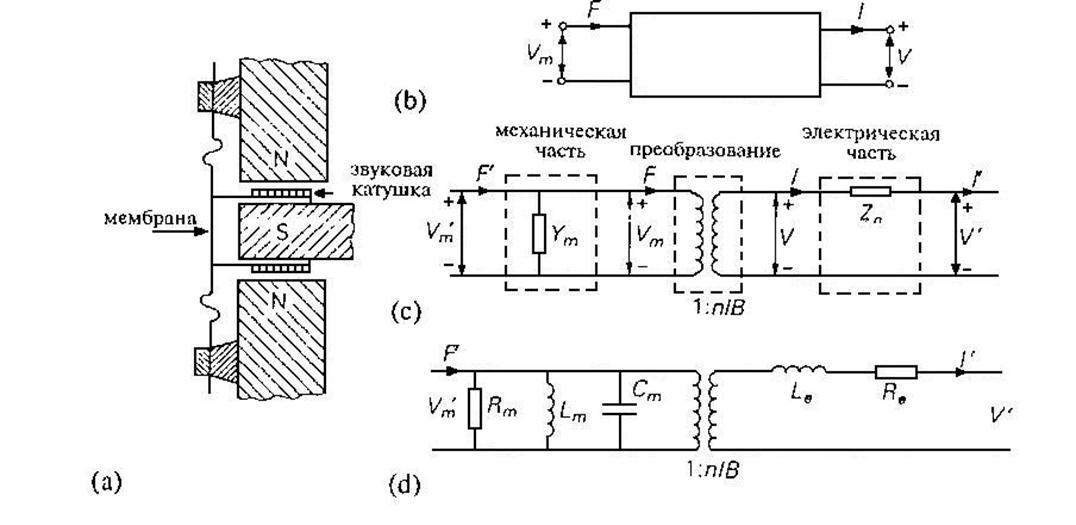
Измерительные приборы в электрических измерениях, страница 3

.

Рис. 3.3. (а) Электродинамический преобразователь. (b) Линейный неоднородный четырехполюсник – аналог преобразователя (а). (с) Трехкаскадный четырехполюсник. (d) Электрический аналог преобразователя (а).

Поскольку определитель этой матрицы равен единице, преобразователь должен быть обратимым.

Его можно использовать как входной преобразователь (микрофон), а также наоборот, в качестве выходного преобразователя (громкоговоритель). Если этот датчик используется как входной преобразователь и к его катушке не подключена нагрузка, то выходное напряжение будет пропорционально скорости движения мембраны. Если этот преобразователь, используемый как выходной, возбуждается некоторым током, а мембрана удерживается неподвижной, так что скоростью можно пренебречь, то сила, действующая на поверхность мембраны, будет пропорциональна току (см. также рис. 3.2.(b)).

Очевидно, что мы можем рассматривать этот идеальный пассивный преобразователь как трансформатор, преобразующий размерность входной величины в соответствующую размерность выходной величины. Коэффициент передачи этого преобразователя размерности равен 1:nlB. Согласно рис. 3.3(с) и учитывая импеданс катушки Z_e, получаем:

Даже если к катушке не подключено сопротивление нагрузки, она будет все-таки оказывать определенное воздействие на мембрану, придавая ей некоторую скорость, что вызвано механическим импедансом Z_m подвижной части преобразователя. С учетом этого можно записать: , когда .

Этот пример демонстрирует один из недостатков V- и I-величин. Механический импеданс равен обратной величине отношения V к I (см. также приложение А.4). Это связано с внесистемным выбором импеданса в механике.

Поэтому переход от V_m, F к V’_m, F’ задается равенством:

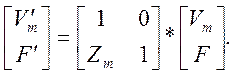
Следовательно, передаточные соотношения для преобразователя в целом принимают вид:

,

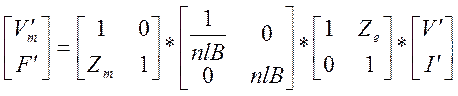и их можно переписать как

.

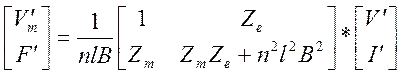В результате в схеме на рис. 3.3(d), импеданс Z_e заменен на сопротивление катушки R_e и включенную последовательно с ним индуктивность катушки L_e. Механическая проводимость Y_m определяется механическим сопротивлением R_m, массой подвижной части мембраны и катушки С_m и механической гибкостью закрепленной части мембраны L_m. Если мы знаем величину каждого параметра, то можем найти передаточную характеристику и определить динамическое поведение. Можно ожидать, что поведение системы зависит от электрического импеданса, которым нагружена звуковая катушка. Аналог, показанный на рис. 3.3(d), позволяет нам к тому же рассчитать входной и выходной импедансы этого преобразователя. Эта информация необходима для правильного согласования преобразователя с объектом измерения и с остальной частью измерительной системы.

3.2.1 Электромеханические датчики

Теперь рассмотрим принцип работы нескольких датчиков, применяемых для измерения механических величин. Мы ограничимся обычными величинами, такими как смещение, ускорение, сила и т. д.

Датчики смещения

Датчики смещения могут измерять как линейный сдвиг (при поступательном движении), так и угол поворота (при вращении). Кроме того, их можно классифицировать в соответствии с используемым принципом преобразования. Например, можно провести различие между резистивными, емкостными, индуктивными и оптическими датчиками поступательного движения или вращения. Эти механические датчики называются также тензодатчиками или сенсорами.

Резистивные датчики смещения

Распространенным типом датчика смещения является потенциометрический датчик. В случае измерения сдвига при поступательном движении он представляет собой, в действительности, не более чем движковый потенциометр. Для измерения угла поворота при вращении можно применить поворотный потенциометр. Проволочные потенциометры обычно имеют большую точность, меньший температурный коэффициент и т. д. Однако конечная разрешающая способность проволочных датчиков смещения ограничивает их возможности. Недостатком всех датчиков потенциометрического типа является механический износ и химическая коррозия, способные изменить передаточную характеристику датчика в течение его срока службы.

В качестве примера датчика линейного смещения приведем in casu параметры проволочного движкового потенциометра, с 1000 витками провода из нихрома (NiCr):

длина – 25 см, полное сопротивление – 300 Ом, нелинейность – 10^-3,  максимальное разрешение – 10³, температурный коэффициент – 2х10^-4 К ^-1, сила трения -0,5 Н.

Легко видеть, что потенциометрический датчик смещения становится нелинейным, когда он нагружен. Относительная ошибка, появляющаяся при подключении нагрузки, равна нулю при х = 0 или х = 1 и максимальна при     х = 0,5 (х – относительное положение подвижного контакта (движка) на длине резистора, так что 0 < х < 1). Когда х = 0,5, относительная ошибка равна – R/4R_l, где R – полное сопротивление потенциометра, а R_l – сопротивление нагрузки.

В другом типе резистивного датчика смещения используется тот факт, что электрическое сопротивление проводника зависит от размеров проводника. Сопротивление R является функцией площади поперечного сечения А проводника, его длины l и удельного сопротивления ρ:

R = R(A, l, ρ).

Если проводник механически растягивается или сжимается, то его параметры А, l и ρ изменяются и, как следствие, меняется R. Это дает возможность измерять очень малые перемещения. На рис. 3.4(а) показан отрезок проволоки (тензодатчик), который удлиняется на величину Δl при прикладывании растягивающих усилий. Используя разложение в ряд, можно вычислить чувствительность этого проволочного датчика деформации:

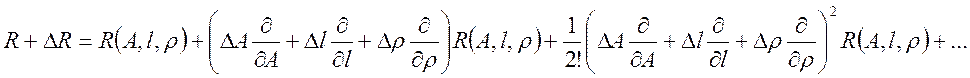
Если каждая из величин ΔА/А, Δl/l, Δρ/ρ меньше 1, а кривизна в точке R(A,l,ρ) мала, то можно пренебречь членами более высоких порядков. Вычитая R=R(A,l,ρ) из обеих частей равенства, получаем следующее дифференциальное уравнение:

.

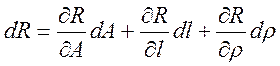При ρ=ρ(l), А=А(d) и d=d(l) это уравнение принимает вид:

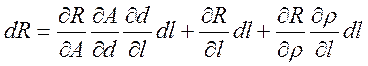
и поэтому:

.

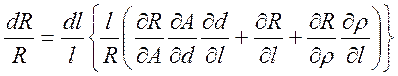Множитель в скобках является точным выражением чувствительности  проволоки к изменению длины. Мы можем найти величину этой чувствительности, используя следующие соотношения:

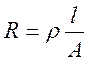 (электрическое сопротивление)