Измерительные приборы в электрических измерениях, страница 17

 

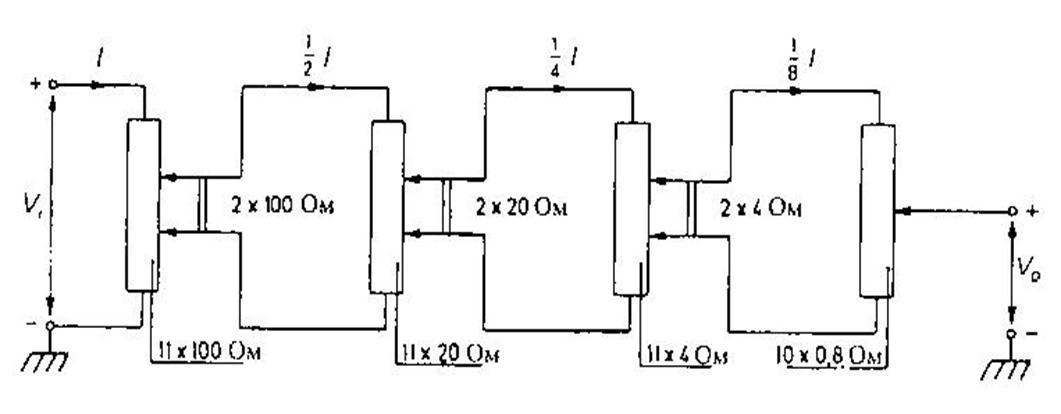
Рис. 3.25. Делитель напряжения Кельвина-Варлея.

характеристического аттенюатора является каскадное соединение нескольких Т-образных звеньев. На рис. 3.26 показано одно Т-образное звено такого аттенюатора. Обычно в этих случаях R_v = R_cи R_l= R_c, где R_v –  сопротивление источника, R_l – сопротивление нагрузки, а R_c – характеристическое сопротивление. Поэтому входное сопротивление Т-образного звена R_iдолжно быть равно R_c, когда к его выходу подключена нагрузка, и выходное сопротивление звена R_oдолжно равняться R_c, когда на его входе включен источник с выходным сопротивлением R_s= R_c. Из условий R_i = R_cи R_o= R_cследует, что R₁=R₂=R_sи R₃=R_p(см. рис. 3.26(b)). Теперь можно найти соотношение между R_sи R_p:

;

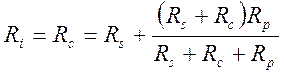таким образом, . Коэффициент передачи напряжения β_vравен

.

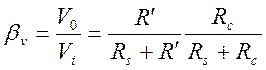При || и  получаем:

.

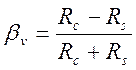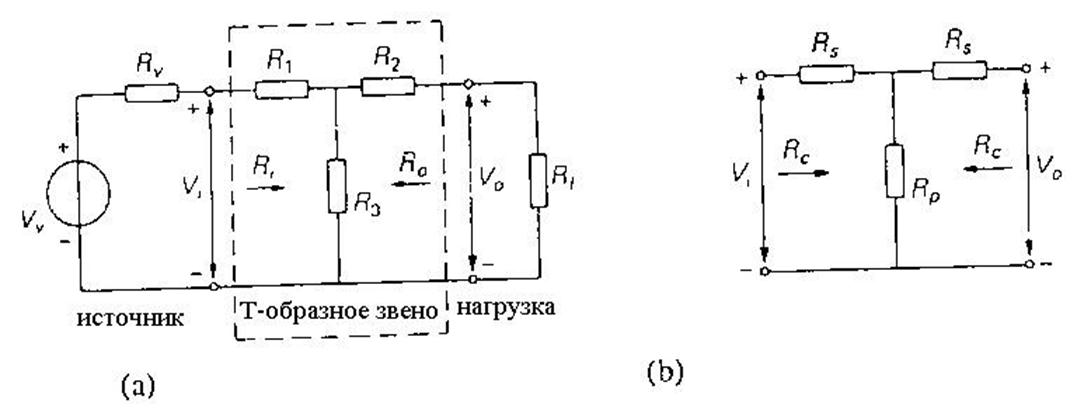
Рис. 3.26. (а) Характеристический аттенюатор, состоящий из одного Т-образного звена. (b) Симметричное Т-образное звено. R_c - характеристическое сопротивление.

Ослабление характеристического аттенюатора чаще всего выражается в децибелах (дБ) (см. Приложение А.З). Выраженный в децибелах, коэффициент ослабления α имеет вид:

,

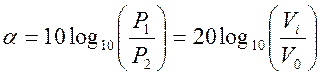поскольку R_v=R_i=R_c=R₀=R_l. Итак, получаем:

[дБ].

Достоинство характеристических аттенюаторов состоит в том, что их звенья можно включать непосредственно одно за другим. Полный коэффициент передачи β_v равен произведению коэффициентов передачи отдельных звеньев. Если ослабление выражено в децибелах, то полное ослабление равно сумме коэффициентов ослабления отдельных звеньев. Поэтому

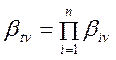 и ,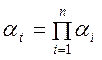

где β_tv– полный коэффициент передачи напряжения, а а₁ – коэффициент ослабления (в дБ) составного характеристического аттенюатора, состоящего из п характеристических звеньев.

В качестве примера приведем параметры характеристического аттенюатора, из трех симметричных Т-образных звеньев: п=3, R_c=60 Ом, β_tv = 1/8 или α₁ = 18 дБ. Таким образом, для одного звена  β_v = 1/2 и а = 6 дБ, так что       R_s= 20 Ом, a R_p=80 Ом. Характеристические аттенюаторы можно также собирать не из Т-образных звеньев, а из п- или Н-образных звеньев (см. рис. 3.27).

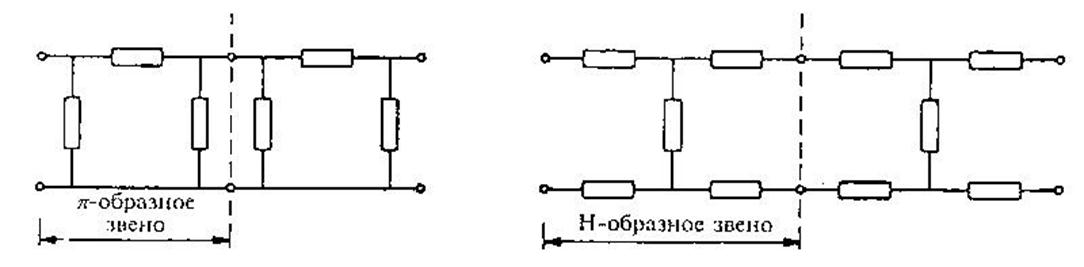
Рис.3.27. Характеристические аттенюаторы, состоящие из π- и Н-образных звеньев.

Измерительные трансформаторы

Для ослабления высоких напряжений и больших токов обычно применяют трансформаторы, поскольку рассеяние мощности резистивными аттенюаторами стало бы чрезмерно большим. Из соображений безопасности предпочтение отдают обычно трансформаторным аттенюаторам, а не индуктивным или емкостным аттенюаторам, так как трансформатор обеспечивает изоляцию между измеряемым объектом и прибором. Измерительные трансформаторы часто применяют не только для измерений в силовых цепях. Например, с помощью трансформаторов часто подают возбуждающее воздействие на «плавающие» мостовые схемы, осуществляют согласование по шуму с низкоимпедансными источниками, с их помощью удается избегать контуров заземления. Кроме того, трансформаторы можно найти в токовых щупах осциллографов, в мультиметрах и во многих других измерительных приборах. В дальнейшем мы ограничимся применением измерительных трансформаторов в силовых цепях.

Рассмотрим сначала идеальный трансформатор (см. рис. 3.28(а)). Действие такого трансформатора выражается следующими соотношениями:

, .

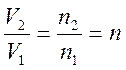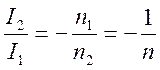Для идеального трансформатора отношение числа витков п полностью определяет как коэффициент передачи напряжения, так и коэффициент передачи тока. Фаза напряжения не изменяется, а фаза тока изменяется на 180°. Хотя, в действительности, это справедливо только отчасти. Отклонение от идеального поведения характеризуется ошибкой значения коэффициента передачи ε и фазовой ошибкой θ.

Ошибка коэффициента передачи напряжения ε_v, по определению, равна:

,

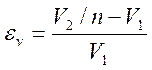а ошибка коэффициента передачи тока ε_i –

,

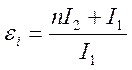так как .

Фазовая ошибка θ_vравна разности фаз между входным и выходным напряжениями. Фазовая ошибка θ_iпри передаче тока равна отклонению разности фаз токов от 180°. Полярность напряжения и направление тока определены так, как показано на рис. 3.28(а). Ошибки коэффициента передачи и фазы вызваны различными паразитными эффектами. Поэтому для того,

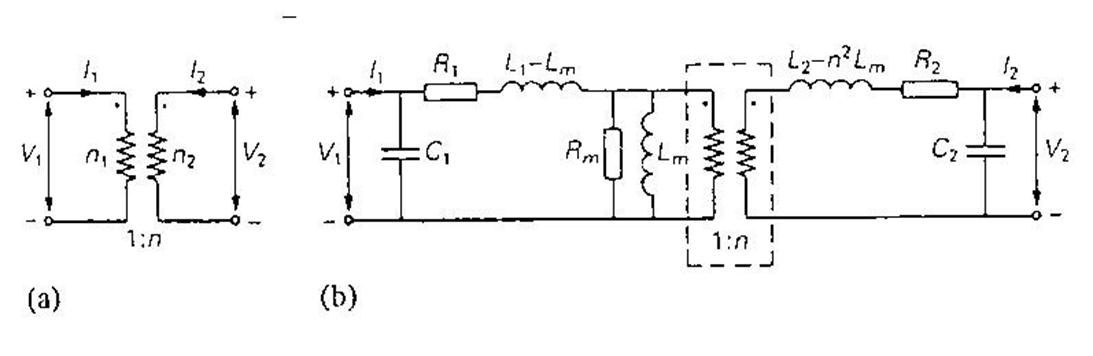
Рис.3.28. (а) Идеальный трансформатор. (b) Более реалистический электрический эквивалент трансформатора.

чтобы получить электрический эквивалент реального измерительного трансформатора, нам необходимо к идеальной модели трансформатора добавить несколько дополнительных импедансов (см. рис. 3.28(b)).

В этой эквивалентной схеме L₁ – индуктивность первичной обмотки, а L₂  – индуктивность вторичной обмотки. Ток намагничивания, создающий магнитный поток в сердечнике, течет через индуктивность L_m, равную , где . Коэффициент связи k определяет долю магнитного потока, создаваемого первичной обмоткой, которая охватывается вторичной обмоткой. Если k = 1, то обе индуктивности и  становятся равными нулю. Эти индуктивности отражают факт потери части магнитного потока вследствие рассеяния (индуктивности рассеяния). Резисторы R₁ и R₂ представляют собой сопротивления первичной и вторичной обмоток (потери в меди), а резистор R_m характеризует потери в сердечнике трансформатора (потери в железе или другом материале сердечника). Наконец, конденсаторы С₁ и С₂ определяют полную емкость обмоток. Обычно емкостями С₁ и С₂ можно пренебречь. Однако на высоких частотах в цепи, содержащей емкость С₂ и индуктивность   может возникнуть резонанс, и это приведет к появлению резонансного пика в частотной характеристике трансформатора. Этот высокочастотный пик иногда называют резонансным пиком рассеяния (пиком, вызванным индуктивностью рассеяния).