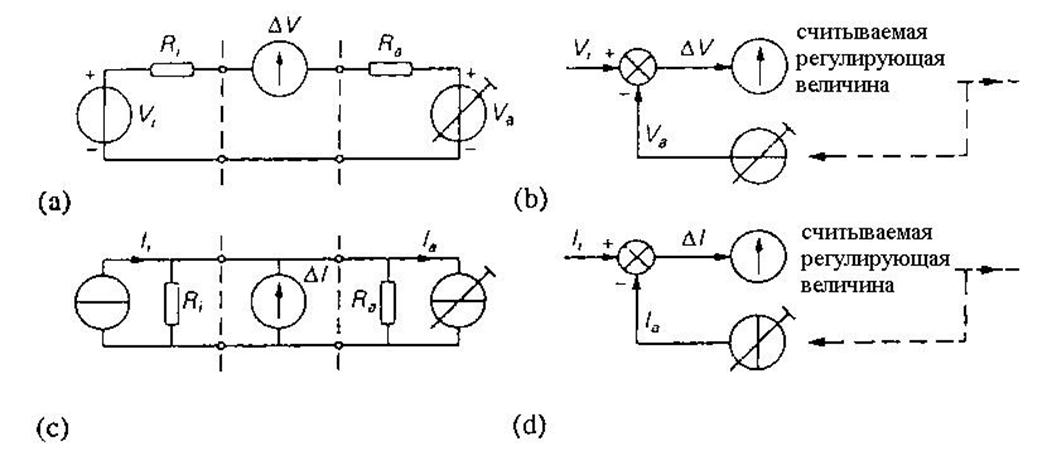
Рис. 3.29. Неавтоматическая компенсация, (а) Компенсация V-величины. (b) Структурная схема при компенсации V- величины, (с) Компенсация I-величины, (d). Структурная схема при компенсации I-величины.
На рис. 3.30(с) в качестве примера автоматической компенсации I- величины показана схема
усилителя «ток-напряжение» (часто неправильно называемого усилителем тока). В
предположении крайне больших значений входного сопротивления Riи коэффициента
усиления А даже малая разность токов ΔI вызвала бы большое
напряжение на входе усилителя, которое после усиления появилось бы на выходе,
имея еще большую величину. Поскольку
величина V0 ограничена напряжением источника питания, входное напряжение и разностный ток ΔI будут очень малыми,
то есть будет выполняться приближенное равенство ![]() .
Компенсирующий ток, создаваемый выходным напряжением, имеющимся на резисторе R2, равен Ia = V0/R2 . При указанных на
рис. 3.30(с) полярности напряжения Vои направлении тока I, коэффициент
передачи равен R2. Соответствующая блок-схема усилителя,
приведенная на рис. 3.30(d), подобна блок-схеме на рис. 3.30(b). В обоих случаях
компенсация входной величины выполнена с применением отрицательной обратной
связи. В структурных схемах на рис.3.29(b) и 3.29(d) также можно увидеть
петлю обратной связи, правда там частью прямой ветви является
человек-наблюдатель. В случае автоматической компенсации
человек-наблюдатель/оператор заменен системой с очень большим коэффициентом
петлевого усиления. Обратную связь можно считать разновидностью непрерывной
автоматической компенсации. Здесь компенсация осуществляется не однократно или в отдельные
моменты времени, а происходит непрерывно.
.
Компенсирующий ток, создаваемый выходным напряжением, имеющимся на резисторе R2, равен Ia = V0/R2 . При указанных на
рис. 3.30(с) полярности напряжения Vои направлении тока I, коэффициент
передачи равен R2. Соответствующая блок-схема усилителя,
приведенная на рис. 3.30(d), подобна блок-схеме на рис. 3.30(b). В обоих случаях
компенсация входной величины выполнена с применением отрицательной обратной
связи. В структурных схемах на рис.3.29(b) и 3.29(d) также можно увидеть
петлю обратной связи, правда там частью прямой ветви является
человек-наблюдатель. В случае автоматической компенсации
человек-наблюдатель/оператор заменен системой с очень большим коэффициентом
петлевого усиления. Обратную связь можно считать разновидностью непрерывной
автоматической компенсации. Здесь компенсация осуществляется не однократно или в отдельные
моменты времени, а происходит непрерывно.
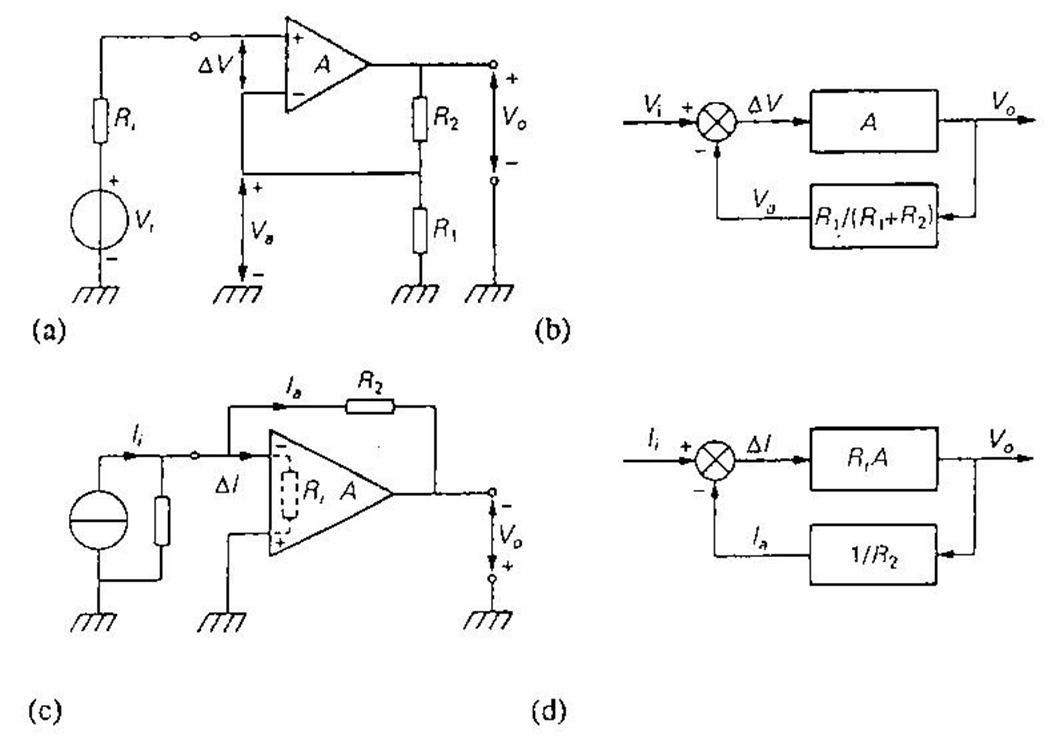
Рис. 3.30.Автоматическаякомпенсация, (а) Компенсация V-величины Vi и (b) соответствующая блок-схема. (с) Компенсация I-величины Ii и (d) соответствующая блок-схема.
3.3.3 Измерительные мосты
При обсуждении методов измерения в главе 2.2 мы видели, что мостовой метод часто применяется для измерения или сравнения импедансов. Эти импедансы могут быть также обобщенными или неэлектрическими. Пример механической мостовой системы приведен на рис. 3.31. Массы т и т' подвешены на двух демпфированных пружинах. Бруску, на котором закреплены пружины, придается скорость V. Разность между скоростями масс Vdизмеряется индуктивным датчиком скорости (см. раздел 3.2.1). Массой этого датчика можно пренебречь. Эквивалентная схема, приведенная на рис. 3.31(b), показывает, что эта конструкция состоит из двух систем «пружина с грузом», подстраиваемых одна под другую (как это делается, например, при регулировке подвески в автомобиле).
Другим примером является конструкция теплового моста, показанная на
рис. 3.32. Области, заполненные точками, обладают тепловым импедансом, равным ![]() , где Ih – тепловой поток
через образец. К сожалению, тепловой поток довольно трудно измерять, поскольку трудно
непосредственно измерить Z, следуя приведенному определению. Поэтому
неизвестный тепловой импеданс Z1 в конструкции на
рис. 3.32 сравнивается с тремя известными тепловыми импедансами Z2, Z3 и Z4. Если к мосту
прикладывается синусоидальное воздействие ΔT и разность
температур (измеренная термопарой) равна нулю, то Z1 можно представить в
виде функции от Z2, Z3, Z4 и частоты возбуждения.
, где Ih – тепловой поток
через образец. К сожалению, тепловой поток довольно трудно измерять, поскольку трудно
непосредственно измерить Z, следуя приведенному определению. Поэтому
неизвестный тепловой импеданс Z1 в конструкции на
рис. 3.32 сравнивается с тремя известными тепловыми импедансами Z2, Z3 и Z4. Если к мосту
прикладывается синусоидальное воздействие ΔT и разность
температур (измеренная термопарой) равна нулю, то Z1 можно представить в
виде функции от Z2, Z3, Z4 и частоты возбуждения.
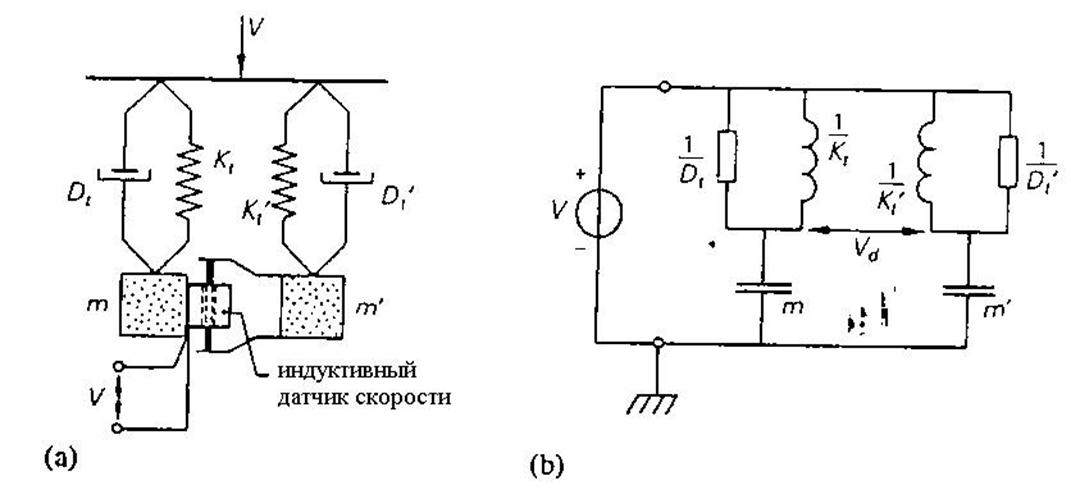
Рис. 3.31. (а) Механическая мостовая конструкция. Разность скоростей масс m и т' преобразуется в электрический выходной сигнал моста. (b) Эквивалентная схема моста, изображенного на рис. (а). V- скорость на входе моста.
В общем случае измерение импедансов основано на применении мостовой схемы с тремя
известными и одним неизвестным импедансом. Один или более из известных
импедансов регулируемые. На рис. 3.33 показано, что мостовую схему можно
рассматривать как четырехполюсник. Входное напряжение Viравно напряжению
источника питания, а выходное напряжение – напряжению на детекторе. Если
внутренний импеданс источника питания пренебрежимо мал по сравнению с ![]() ||
||![]() ,
а импеданс нуль-детектора
много больше, чем (Z1||Z4)+(Z2||Z3), то легко найти выражение
для коэффициента передачи схемы. Напряжение на детекторе равно
,
а импеданс нуль-детектора
много больше, чем (Z1||Z4)+(Z2||Z3), то легко найти выражение
для коэффициента передачи схемы. Напряжение на детекторе равно
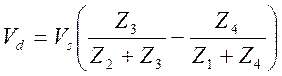 .
.
Мост сбалансирован, когда коэффициент передачи равен нулю (состояние баланса или нулевое состояние), то есть при условии:
Поэтому нулевое состояние достигается при
![]() .
.
Видно, что нулевое условие не зависит от напряжения возбуждения моста Vs. Оно также никак не связано с импедансом возбуждающего мост источника или импедансом детектора. Тот факт, что импеданс моста не оказывает влияния, является результатом баланса моста, когда напряжение на детекторе равно нулю. Результат, состоящий в том, что нулевое состояние не зависит от импеданса источника, можно объяснить тем, что наличие конечного импеданса источника только уменьшит напряжение на входе моста Vi, поскольку напряжение источника поделится между импедансом источника и входным импедансом моста.
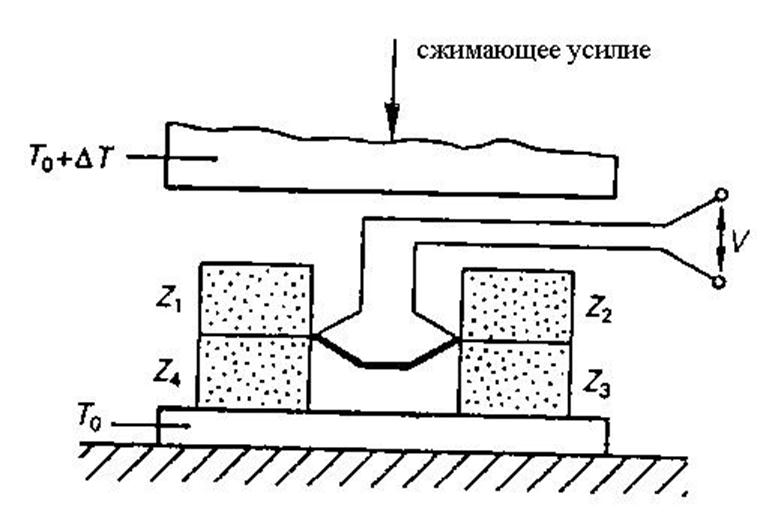
Рис. 3.32. Конструкция теплового моста. Т0 - температура окружающей среды, ΔT- температура возбуждения моста.
Важным параметром моста для измерения импедансов является его чувствительность. Чувствительность моста определяется величиной напряжения на нуль-детекторе или величиной тока, протекающего через него, при небольшом отклонении от состояния баланса. Тогда в предположении, что мост балансируется с помощью регулируемого импеданса Z1(рис. 3.33), дифференциальную чувствительность Sdiffдля напряжения детектора Vdможно записать в виде:
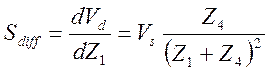 .
.
Так как абсолютная величина Z1 может отличаться от моста к мосту, нас больше интересует чувствительность напряжения Vdк относительному изменению dZ1/Z этого импеданса Z1. В этом случае получаем:
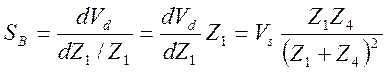 .
.
Если мы теперь введем параметр моста F(=Z2/Z3) с учетом, конечно, того, что при балансе моста F=Z1/Z4, то чувствительность SB примет вид:
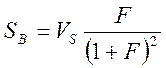 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.