![]() .
.
Очевидно, что имеются три метода реализации емкостного датчика смещения: можно изменять d, А или ε. Эти три метода проиллюстрированы на рис. 3.6. Если выбрать конденсатор с плоскими параллельными пластинами, разнесенными на расстояние х и пренебречь всеми краевыми эффектами, то емкость такого датчика с параллельными пластинами равна:
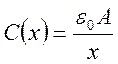 .
.
Однако, этот датчик нелинеен и имеет гиперболическую передаточную характеристику, как показано на рис. 3.6(а). Этот тип датчика часто применяют для измерения малых приращений смещения без контакта с измеряемым объектом. Характеристика датчика обычно линеаризуется путем применения балансной схемы. Пример уже был дан на рис. 3.1(b).
Если у плоского конденсатора изменяется площадь электродов, то получаем:
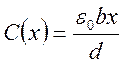 .
.
Теперь датчик имеет линейную зависимость от х. Обычно этот тип датчика реализуется в виде поворотного конденсатора для измерения угловых смещений, а не в виде варианта со сдвигом, приведенного на рис. 3.6(b). Конструкция с поворотным конденсатором применяется также в качестве выходного преобразователя для измерения электрических напряжений (емкостной вольтметр).
Для плоского конденсатора изменение положения диэлектрика приводит к следующему результату:
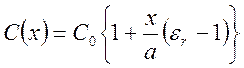 ,
,
где
![]() . Этот датчик также линеен. Он бывает
линеаризован, главным образом, в форме двух концентрических цилиндров и используется
для измерения уровня жидкости в резервуаре. Непроводящая жидкость играет роль
диэлектрика.
. Этот датчик также линеен. Он бывает
линеаризован, главным образом, в форме двух концентрических цилиндров и используется
для измерения уровня жидкости в резервуаре. Непроводящая жидкость играет роль
диэлектрика.
Сила, которую измеряемый объект должен приложить к емкостному датчику, чтобы переместить электроды, очень мала. Будем полагать эту силу F(x) положительной, когда она имеет направление, при котором х увеличивается. Если пренебречь всеми потерями (из-за трения, сопротивления и т. д.), то отдаваемая измеряемым объектом механическая энергия dEm, при бесконечно малом смещении dx, плюс электрическая энергия dEe, подводимая подключенным к датчику источником питания с
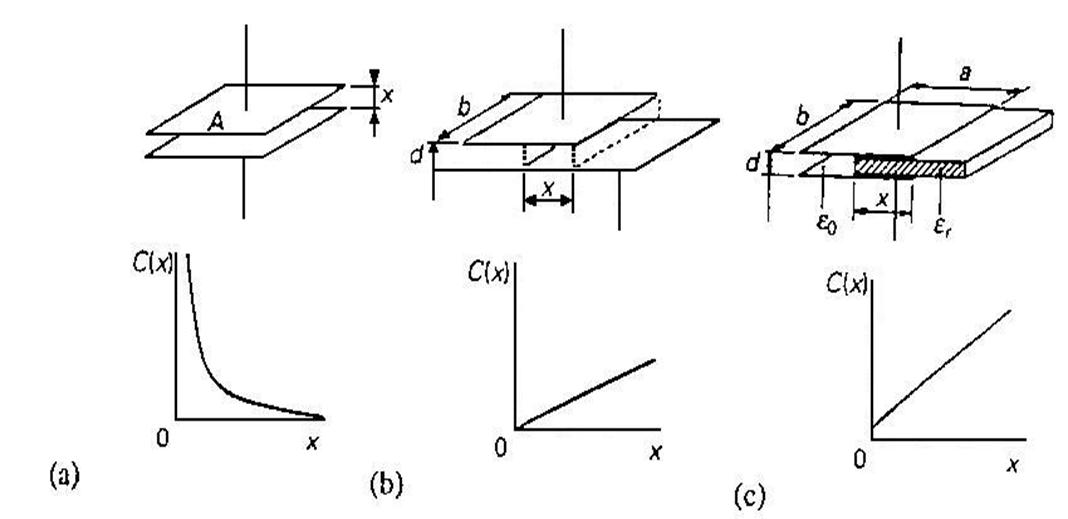
Рис. 3.6 Емкостной датчик смещения: (а) с изменяемым расстоянием между электродами; (b) с изменяемой площадью электродов; (с) с изменяемым диэлектриком.
напряжением V, должны быть равны увеличению энергии электрического поля dEf между электродами конденсатора. Баланс энергии может быть записан как:
![]() ,
,
где
![]() ,
,
![]() ,
,
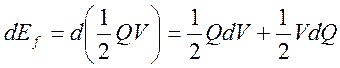 .
.
Следовательно, для датчика, приведенного на рис. 3.6(а), сила положительна, а для датчиков на рис. 3.6(b) и на рис. 3.6(с) – отрицательна. Таким образом, если подвижный электрод имел полную свободу перемещения, то он займет положение, при котором емкость максимальна. Если С – линейная функция от х, то сила F не зависит от х.
Силы Кулона чрезвычайно малы. Линейный емкостной датчик смещения с емкостью 100 пФ, имеющий диапазон измерения 1см, при напряжении питания 10 В требует усилия всего лишь 0,5 мкН!
При вычислении емкости С(х) для трех случаев, показанных на рис. 3.6, не учитывались краевые (или концевые) эффекты в конденсаторах. Эти краевые эффекты можно подавить, используя экранирующий электрод, как показано на рис. 3.7. Датчик смещения С, снабжен здесь заземленным экранирующим электродом, расположенным так, что электрическое поле внутри конденсатора однородно на указанных участках ( на краях). Если бы мы измеряли только емкость между подвижным и неподвижным электродами и при этом не учитывали емкость электродов относительно экрана, то датчик был бы свободен от возмущающих краевых эффектов. В схеме, приведенной на рис. 3.7(b), это достигается путем соединения экрана со средней точкой трансформатора, входящего в состав моста. Напряжение, приложенное к индикатору, может быть сделано равным нулю путем балансировки моста переменным конденсатором Cn. В этом случае экран имеет потенциал земли. Поскольку емкость между незаземленным электродом конденсатора С1, и экраном включена параллельно верхней половине вторичной обмотки трансформатора моста, то она не влияет на условие баланса моста: С1 = Cn.
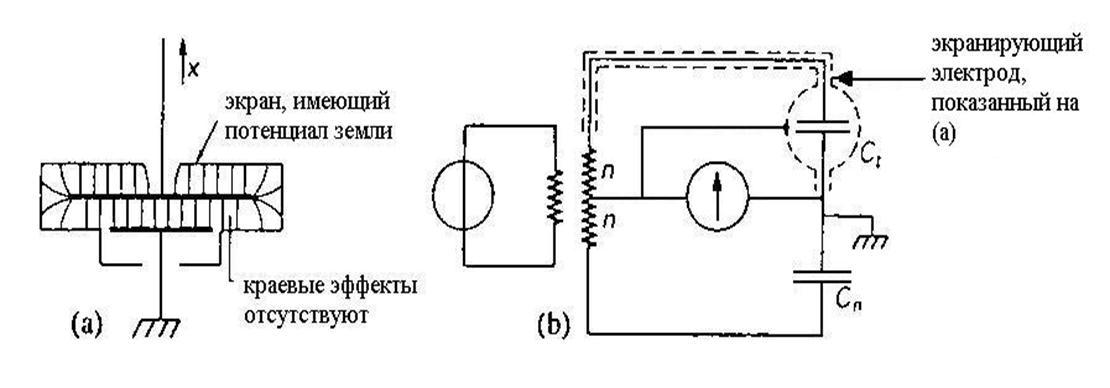
Рис. 3.7. Конструкция экранирующего электрода для подавления краевых эффектов в емкостном датчике.
Часто емкостной датчик смещения уже включен в мостовую схему, предназначенную для измерения емкости и, следовательно, для измерения смещения. Другая возможность состоит в использовании конденсатора в качестве элемента, определяющего частоту колебаний генератора. Тогда значение частоты является мерой смещения. Емкостные датчики надежны и дешевы. Примером акустического измерительного датчика является конденсаторный микрофон, который – благодаря своей высокой чувствительности, большому динамическому диапазону, широкой полосе частот и плоской частотной характеристике (30 кГц по уровню 1 дБ) – часто используется при измерениях уровня звука.
Индуктивные датчики смещения
Имеется возможность изменять как самоиндукцию одиночной катушки при ее смещении, которое должно быть измерено, так и взаимоиндукцию двух катушек при изменении связи между ними вследствие смещения. Очевидным способом влияния на индуктивность катушки является изменение действующего числа ее витков. Этот принцип схематически изображен на рис. 3.8(а). Другой метод показан на рис. 3.8(b), где индуктивность изменяется путем варьирования магнитного сопротивления сердечника с помощью воздушного зазора переменной ширины.
Если в первом датчике мы игнорируем ту часть витков, которая расположена вне сердечника (это можно сделать, если магнитная проницаемость μ велика, а воздушный зазор, через который проходит катушка, узкий), то для обоих датчиков имеем:
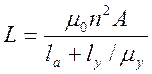 .
.
В этом выражении n – число витков катушки, А – площадь поперечного сечения сердечника, la – ширина воздушного зазора, ly – длина магнитного пути по сердечнику и якорю, а μy – относительная магнитная проницаемость ферромагнитного материала сердечника. В первом варианте (рис. 3.8(а)) изменяется только n как функция х, поэтому:
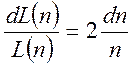 .
.
Во втором варианте (рис. 3.8(b)) изменяется только la. При la=2x зависимость становится гиперболической относительно х:
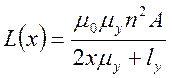 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.