Измерительные приборы в электрических измерениях, страница 32

На рис. 3.63(b) показана простая реализация ЦАП. Цифровой вход Dсостоит из всех битов а_i(i = 0, 1, , п). Если а_i = 1, то соответствующий переключатель а_iподключен к отрицательному опорному напряжению – V_r; если же a_i = 0, то переключатель подключен к земле. Так как коэффициент усиления операционного усилителя без обратной связи А₀ очень велик, в узле Sреализуется состояние виртуального замыкания. Ток во входной цепи этого усилителя, преобразующего ток в напряжение, равен сумме токов, протекающих по всем резисторам R_i, для которых а_i= 1. Этот ток равен

.

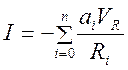Следовательно, аналоговое выходное напряжение равно V_A= -IR. Для того, чтобы выполнялось равенство: V_a=V₀D, мы выбираем сопротивление резистора R_i вдвое больше сопротивления последующего резистора R_i+1. Так, если R_о= R, то R₁= R/2, R₂ = R/4 и R_i =2^-iR. Тогда для V_Анаходим:

.

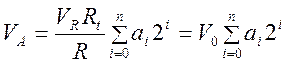У преобразователя с 11-битовым входом п = 10. При V_R=5 В, R_f=1 кОм и R₀ = R= 1 МОм наименьший шаг приращения напряжения V₀ = 5 мВ. Наименьшее сопротивление имеет резистор R_l0; оно соответствует старшему разряду а₁₀ и должно быть в 2¹⁰ раз меньше, чем сопротивление резистора R₀, то есть R₁₀ = 1 / 1024 МОм. (Здесь следует иметь в виду, что i – это нижний индекс в обозначении отдельных разрядов а_i: i = 0, 1, 2, , n. Так что всего имеется  n+ 1 бит!)

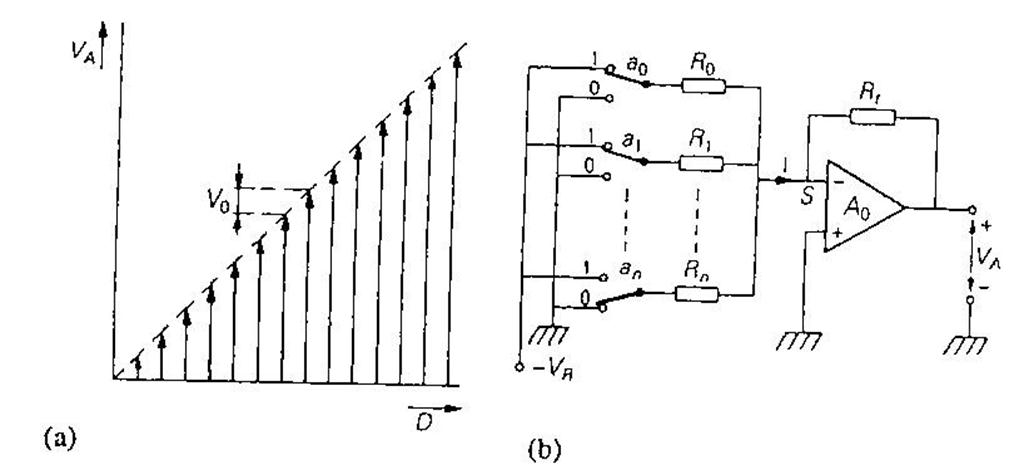
Рис. 3.61. (а) Передаточная характеристика ЦАП. (b) Реализация ЦАП, в котором сопротивление каждого резистора R_i соответствует весу двоичной цифры или бита.

Основной недостаток такого ЦАП состоит в том, что соотношение между наибольшим сопротивлением (R₀) и наименьшим (R_n) становится слишком большим с практической точки зрения, когда число бит велико. При n + 1 битах это отношение равно R₀/R_n = 2ⁿ. Когда размеры резисторов малы (например, при изготовлении их методом тонкопленочной технологии), трудно точно обеспечить требуемую величину сопротивления в таком широком диапазоне значений. Резисторы с наименьшими сопротивлениями R_n, R_n-1, которые соответствуют битам с наибольшим весом а_n, а_n-1, должны быть определены особенно точно по отношению к резистору обратной связи R_f.

Разрешающая способность ЦАП равна отношению максимального выходного напряжения к шагу приращения напряжения V₀. Таким образом, разрешение r равно:

.

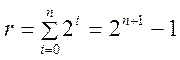Очевидно, что разрешение ЦАП должно быть достаточно высоким, чтобы обеспечить требования, предъявляемые к точности измерительной системы. Если бы сопротивления всех резисторов ЦАП были выдержаны с исключительно высокой точностью, но разрешающая способность была бы низкой, то точность GAIT полностью определялась бы большой ошибкой квантования, как следствие низкого разрешения. Если допустимую относительную погрешность значения V_a = V₀D обозначить через ε, то разрешающая способность должна удовлетворять неравенству: r≥1/ε .

Погрешность ЦАП, изображенного на рис. 3.61(b), с указанными выше сопротивлениями резисторов может достигать приблизительно 10^-3. Это требует разрешения 10³, то есть по крайней мере 10 битов, поскольку 2¹⁰ – 1 = 1023.

На рис. 3.62 приведена схема ЦАП, в которой используются резисторы только двух различных номиналов. Схема состоит из резисторной матрицы и усилителя, преобразующего ток в напряжение. Очевидно, что сопротивление участка матрицы вправо от узлов 0, 1, 2, , n остается одним и тем же (равным 2R), независимо от номера узла, так как потенциал в точке переключения всегда равен потенциалу земли (независимо от того, установлено а_i = 0 или а_i=1). Как следствие, ток в каждом узле 0, 1, 2, , n будет делиться поровну между равным 2R сопротивлением вправо от узла и резистором с сопротивлением 2R, подключенным к переключателю. Ток, текущий от источника опорного напряжения V_R к n-му узлу равен  -V_R/ R. В этой точке он делится поровну на два тока величиной - V_R / R, причем один из них течет через переключатель, положение которого определяется значением бита а_n, а другой – в остальную часть матрицы вправо от этого узла. Этот процесс повторяется в (n - 1)-м узле, так что ток через резистор и переключатель, относящийся к биту а_n-1, становится равным  - V_R / 4R и т. д. Эти токи суммируются на виртуально заземленном входе операционного усилителя. Ток, соответствующий младшему разряду а₀, равен –V_R/2ⁿ⁺¹R, и им определяется минимально возможный шаг напряжения V₀на выходе. Для этого минимального шага получаем: V₀ = V_R/2ⁿ; следовательно, функция передачи ЦАП в целом равна:

.

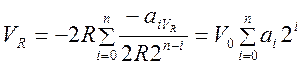В этой схеме требуется, чтобы отношение сопротивлений резисторов Rи 2Rрезисторной матрицы, относящихся к старшим битам а_п, а_п-1, , к сопротивлению резистора обратной связи 2Rвыдерживалось точно. Так как здесь ислользуются только два номинала резисторов, у такого ЦАП точность может быть гораздо большей, чем в предыдущем случае. Достижима погрешность ниже 10^-4. Хотя в этом случае нам необходимо обеспечить, по крайней мере, 14-битное разрешение, так как 2¹⁴= 16384.

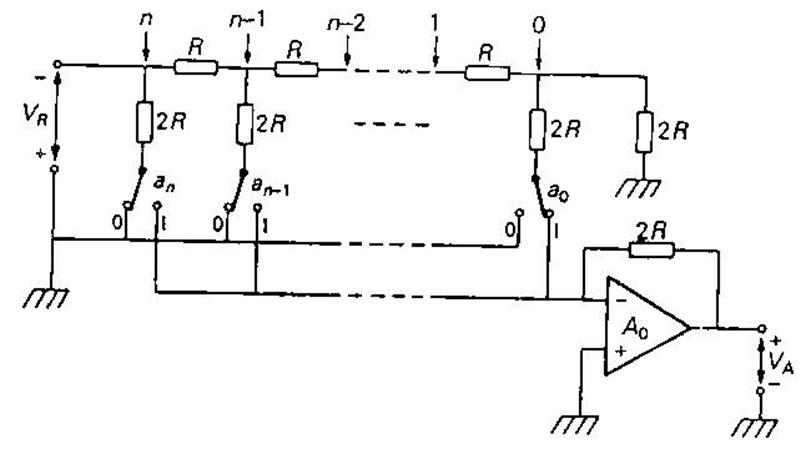
Рис. 3.62. Цифро-аналоговое преобразование, с использованием резисторной матрицы.

Аналого-цифровое преобразование

Математически аналого-цифровое преобразование описывается так

.

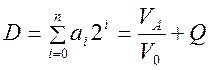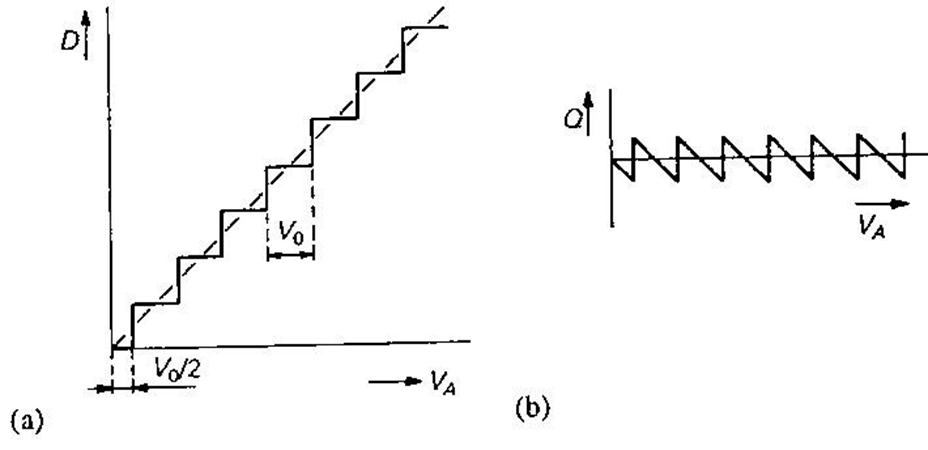
Рис. 3.63. (а) Передаточная характеристика АЦП. (b) Ошибка квантования Q, которой всегда сопровождается аналого-цифровое преобразование.

Здесь V_A – преобразуемое входное напряжение, V₀ – минимально различимый шаг напряжения и Q– остаток, который возникает из-за ошибки квантования. Задача аналого-цифрового преобразователя (АЦП) состоит в том, чтобы найти такие значения битов а_i, при которых ошибка квантования Qминимальна. Очевидно, следует ожидать, что ошибка квантования всегда не равна нулю: напряжение V_Aпредставляет собой сигнал с непрерывным множеством значений, в то время как Dможет принимать только дискретные значения (см. рис. 3.63(а)).

Наиболее точные АЦП реализуются с применением метода автоматической компенсации (см. раздел 3.3.2). Они могут быть выполнены с включением ЦАП в цепь обратной связи так, чтобы выходное напряжение ЦАП компенсировало входное напряжение V_A. Если входное напряжение компенсируется непрерывно, то такой АЦП называют следящим АЦП (см. рис. 3.64(а)).