Уравнения автоматических систем. Описание систем в пространстве состояний. Динамические характеристики автоматических систем

Математическое описание автоматических систем.

Уравнения автоматических систем (АС)

Различают два вида уравнений, которыми могут быть описаны свойства автоматических систем: уравнения статики и уравнения динамики.

Уравнения статики – это зависимость между параметрами системы в установившемся режиме.

Уравнения статики имеют вид: , где - входная величина объекта управления или системы, - выходной параметр.

Уравнения динамики -  это зависимость между параметрами системы во времени, то есть  с учетом предистории этих параметров. Уравнения динамики имеют вид:  или , с начальными условиями: . Начальные условия представляют собой численные значения параметров системы в момент времени .

Рассмотрим алгоритм составления уравнений динамики автоматической системы.

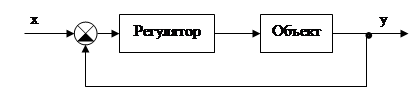
1. Составляем зависимость между входными и выходными параметрами всей системы или ее части на основе различных законой физики. Получаем в общем виде дифференциальное уравнение динамики:

2. Дифференциальное уравнение (1) записываем в отклонениях и проводим его линеаризацию. Каждому параметру дифференциального уравнения даем приращение относительно значения в установившемся режиме:

Подставим выражение (2) в дифференциальное выражение (1) и получаем дифференциальное уравнение в отклонениях:

Линеаризацию осуществляем разложением дифференциального уравнения (3) в сокращенный ряд Тейлора . Получим:

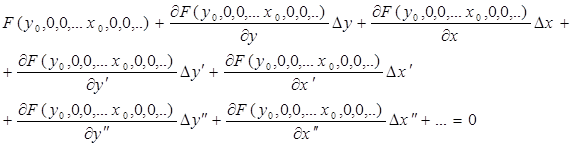
Линеаризация исходного дифференциального уравнения необходима для использования методов решения линейных дифференциальных уравнений, так как общих методов решения нелинейных дифференциальных уравнений не существует.

3. Из уравнения динамики (1) получаем уравнение статики, приравнивая все производные к нулю. в установившемся режиме уравнение статики имеет вид:

4. Вычтем из уравнения (4) уравнение (5). Обозначим значения частных производных коэффициентами  для выходных параметров и  для входных величин. получим дифференциальное уравнение:

Обозначая  из уравнения (6) получим:

Уравнение (7) – это дифференциальное уравнение с постоянными коэффициентами, описывающее динамику системы.

Пример. Составить уравнение динамики для бака со свободным сливом. Входным воздействием для этого объекта является расход воды на входе , выходным параметром – уровень воды в баке .

Площадь поперечного сечения в баке обозначим . Запишем уравнение бака:

, где  - приращение времени,  -  приращение уровня. При уравнение (1) будет иметь вид: , откуда

Расход воды зависит только от уровня воды в баке: . Тогда уравнение (2) будет иметь вид:

Уравнение (3) – это уравнение динамики объекта управления. После линеаризации этого уравнения  в отклонениях получим:

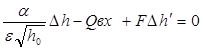
Из уравнения (4) после преобразований согласно алгоритму, получим:

 или 

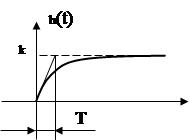Решение уравнения (5) состоит из двух составляющих: . Характеристическое уравнение дифференциального уравнения (5) имеет вид: .

, . Тогда . Учитывая начальные условия: .

Коэффициент равен отношению выходной величины к входному сигналу в установившемся режиме.

Пусть выходной параметр в установившемся режиме равен , тогда 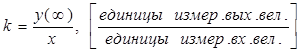. Коэффициент называется коэффициентом передачи. - это постоянная времени. Ее размерность . Постоянная времени характеризует инерционность объекта управления: чем больше ее численное значение, тем более инерционен объект управления.

Пример. Составить уравнение динамики для объекта управления, составленному из двух баков со сливом. Входной параметр , выходной - .

Уравнение первого бака:

.

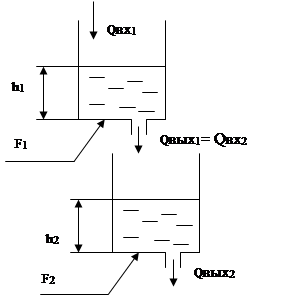
Так как 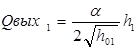 , тогда .

Подставим уравнение (2) в дифференциальное уравнение (1), получим:

.

Запишем уравнение второго бака:

Подставим дифференциальное уравнение (4) в уравнение (3) и найдем уравнение, описывающее динамику объекта управления.

Вопросы.

1.  В чем отличие уравнений статики от уравнений динамики?

2.  Какие должны быть начальные условия в уравнениях дтнамики? А в уравнениях статики?

3.  Почему нелинейные дифференциальные уравнения необходимо преобразовывать к линейному виду?

4.  Поясните термин “инерционность объекта управления”. От каких параметров она зависит? Зависит ли она от - коэффициента передачи?

5.  В чем отличие и ? В чем измеряется ?

6.   Как определить  численно?

7.  Как получить уравнение статики из уравнения динамики? Какие должны быть начальные условия в уравнении статики?

8.  Каково структурное отличиедифференциального уравнения динамики

9.  Что является входным и выходным параметром для АСР?

Описание систем в пространстве состояний

Аналитические свойства системы могут быть описаны в виде системы дифференциальных уравнений в форме Коши:

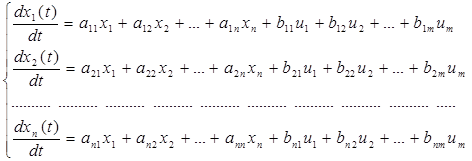
Набор переменных  однозначно и единственным образом описывает систему в любой момент времени. Переменные  называются переменными состояния. в матричном виде систему (1) можно представить: