Уравнения автоматических систем. Описание систем в пространстве состояний. Динамические характеристики автоматических систем, страница 9

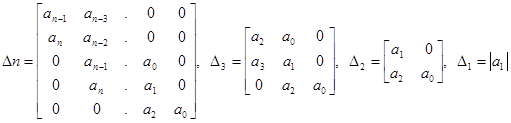
Формулировка критерия Гурвица.

Для устойчивости ситемы необходимо и достаточно, чтобы все определители Гурвица  были положительны:  для  при .

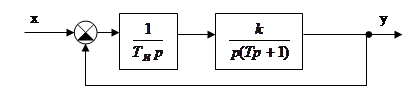
Пример: Определить устойчивость системы.

.

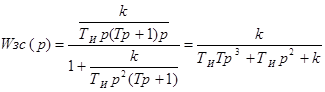Характеристическое уравнение имеет вид: .

, т.к. всегда

             

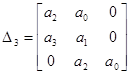
Так как , то система будет неустойчивой.

Рассмотрим в общем виде систему I-го порядка. Характеристическое уравнение .

Согласно критерию Гурвица для устойчивой системы I-го порядка необходимо и достаточно, чтобы  и , т.е. коэффициенты характеристического уравнения были положительными.

Систама II-го порядка имеет характеристическое уравнение вида: .

, т.е. необходимо и достаточно, чтобы . Следовательно, для устойчивой системы  II-го порядка необходимым и достаточным условием являются положительные коэффициенты характеристического уравнения.

.

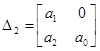Система III-го порядка имеет характеристическое уравнение: .

.   

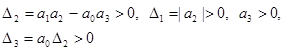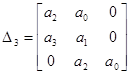
Тогда . Из того, что  следует, что .

Значит для устойчивой системы III-го порядка необходимо и достаточно, чтобы коэффициенты характеристического уравнения были положительны и .

Пример 1: Определить устойчивость системы.

.

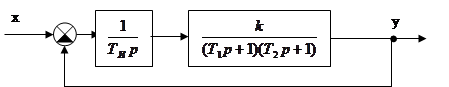
Характеристическое уравнение: .

1.  для .

2. .

Пример 2: Определить устойчивость системы.

	х						y

 

.

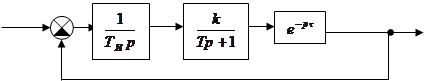
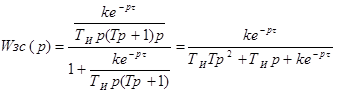Характеристическое уравнение: .

Вывод. Критерий устойчивости Гурвица  не применим для систем с запаздыванием.

Критерий устойчивости Михайлова

Пусть характеристическое уравнение системы имеет вид: .

Выполнив подстановку  получим функцию Михайлова:

Формулировка критерия Михайлова.

Для устойчивости системы необходимо и достаточно, чтобы при изменении частоты w от 0 до ¥ годограф Михайлова обходил последовательно n квандрантов комплексной плоскости, начиная с первого, и нигде не обращаяся в нуль.

Альтернативная формулировка критерия Михайлова.

Для устойчивости системы  необходимо и достаточно, чтобы корни вещественной и мнимой составляющей функции михайлова  и  были вещественными и перемежаемыми.

Перемежаемость корней означает ситуацию, когда с ростом корней по величине  должны поочередно принадлежать уравнениям   и .          

<<<<<.

Пример 1: Определить соотношение параметров системы, при  которой она будет устойчивой, если: .

		х						y

 

.  

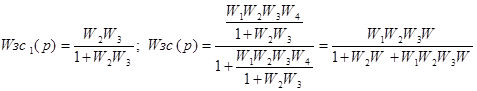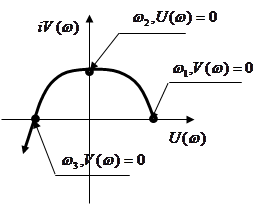
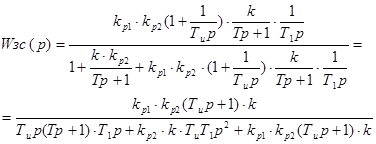
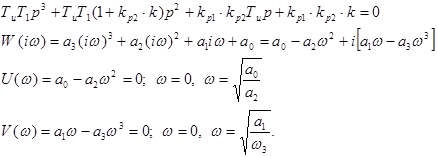
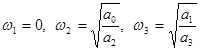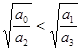Значит, для установившейся системы необходимо: , т.е.  или , или , или .

Подставляя параметры, получим:

Пример 2: Определить устойчивость системы.

	х						y

 

.

.

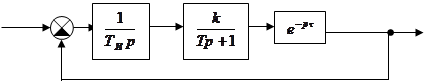
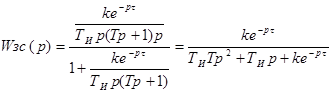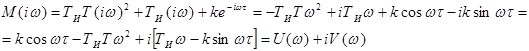Устойчивость системы можно определить, построив годограф Михайлова, либо анализируя корни уравнений   и  в соответствии с альтернативной формой критерия устойчивости Михайлова.

Критерий устойчивости Найквиста