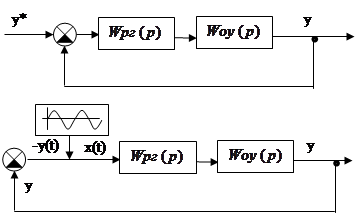
 Пусть разомкнутая система с передаточной функцией
Пусть разомкнутая система с передаточной функцией ![]() будет устойчива или нейтральна.
Разомкнем систему и подадим на ее вход гармонические колебания:
будет устойчива или нейтральна.
Разомкнем систему и подадим на ее вход гармонические колебания: ![]() . На выходе системы установятся
колебания вида:
. На выходе системы установятся
колебания вида: ![]() .
.
Для устойчивости
вистемы важго исследовать случай, когда сигналы ![]() и
и ![]() совпадают по фазе, то есть
совпадают по фазе, то есть ![]() имеет сдвиг по фазе относительно
имеет сдвиг по фазе относительно ![]() , равный
, равный ![]() .
.
Пусть на частоте
![]() фазо-частотная характеристика
разомкнутой системы
фазо-частотная характеристика
разомкнутой системы ![]() .
.
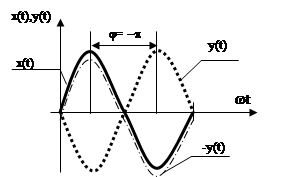 1. Если амплитудо-частотная характеристика
разомкнутой системы
1. Если амплитудо-частотная характеристика
разомкнутой системы ![]() , то в случае замыкания
разомкнутой системы колебания при прохождении через
, то в случае замыкания
разомкнутой системы колебания при прохождении через ![]() и
и ![]() увеличаться по амплитуде, так как
увеличаться по амплитуде, так как ![]() . Со следующим циклом прохождения
сигнала амплитуда увеличивается еще больше, то есть замкнутая система будет
неустойчива.
. Со следующим циклом прохождения
сигнала амплитуда увеличивается еще больше, то есть замкнутая система будет
неустойчива.
2. Если ![]() , тогда при замыкании разомкнутой
системы колебания от цикла к циклу будут уменьшаться по амплитуде, то есть
замкнутая система будет устойчивой.
, тогда при замыкании разомкнутой
системы колебания от цикла к циклу будут уменьшаться по амплитуде, то есть
замкнутая система будет устойчивой.
3. ![]() , тогда при замыкании разомкнутой
системы в замкнутой системе установятся незатухающие колебания, то есть система
будет находиться на границе устойчивости.
, тогда при замыкании разомкнутой
системы в замкнутой системе установятся незатухающие колебания, то есть система
будет находиться на границе устойчивости.
Частная формулировка критерия устойчивости Найквиста.
Если разомкнутая
система является нейтральной или устойчивой, то в замкнутом состоянии она будет
устойчивой, если АФХ разомкнутой системы ![]() не
охватывает точку
не
охватывает точку ![]() .
.
Общая формулировка критерия Найквиста.
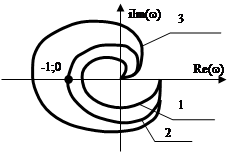 Если разомкнутая система является неустойчивой, то в замкнутом
состоянии она будет устойчивой, если АФХ разомкнутой системы
Если разомкнутая система является неустойчивой, то в замкнутом
состоянии она будет устойчивой, если АФХ разомкнутой системы ![]() охватывает точку
охватывает точку ![]() под углом
под углом ![]() ,
где
,
где ![]() - число корней характеристического
уравнения разомкнутой системы в правой полуплоскости.
- число корней характеристического
уравнения разомкнутой системы в правой полуплоскости.
Кривая 1 – АСР устойчива;
Кривая 2 – АСР на границе устойчивости;
Кривая 3 – АСР неустойчива.
Пример.
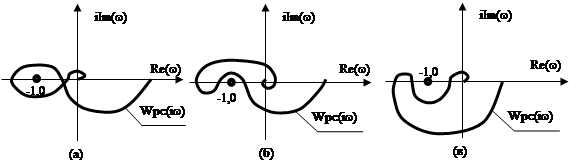
Рис. (а).
Разомкнутая
система неустойчива, имеет два корня в отрицательной полуплоскости, ![]() охватывает точку (-1,0) под углом 2p, значит замкнутая система будет устойчива.
охватывает точку (-1,0) под углом 2p, значит замкнутая система будет устойчива.
Рис. (б), (в), (г).
Замкнутая автоматическая система регулирования устойчива, разомкнутая система – также.
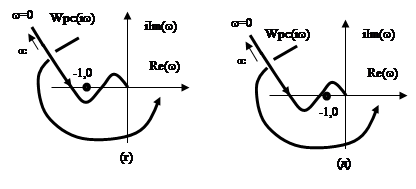
Рис. (д). Замкнутая АСР неустойчива, разомкнутая АСР устойчива.
Формулировка критерия устойчивости Цыпкина.
Если разомкнутая
система является неустойчивой, то в замкнутом состоянии она будет устойчивой,
если число положительных переходов АФХ разомкнутой системы больше, чем число
отрицательных переходов на k/2 при изменении ![]() от
0 до
от
0 до ![]() ,
где k- число положительных корней характеристического
уравнения разомкнутой системы
,
где k- число положительных корней характеристического
уравнения разомкнутой системы ![]() .
.
Под
положительным переходом понимается пересечение АФХ разомкнутой системы отрезка ![]() сверху вниз.
сверху вниз.
Пример 1.
Определить значение коэффициента передачи k , при котором система выходит на границы устойчивости.
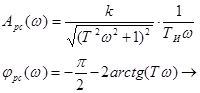
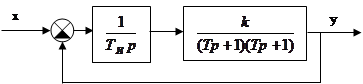
![]()
![]()
Пример 2.
Определить устойчивость системы.
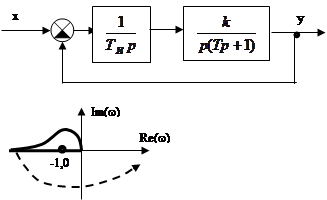
Замкнутая АСР структурно неустойчива. Необходимо определить, устойчива ли разомкнутая система.
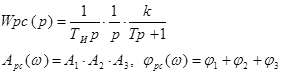
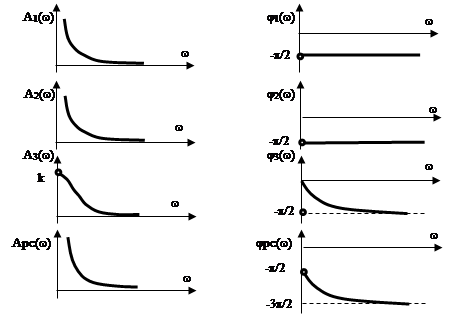
Пример 3.
Определить
значение коэффициентов передачи герулятора ![]() ,
при котором система выходит на границы устойчивости.
,
при котором система выходит на границы устойчивости.
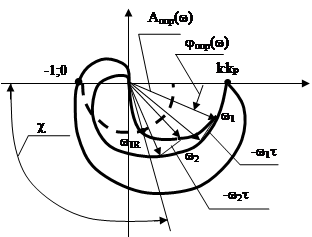
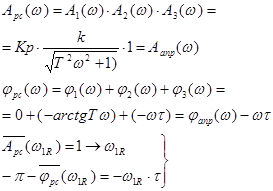
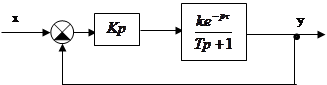
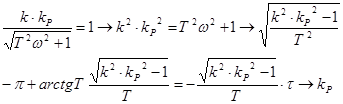
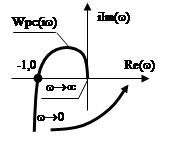
Влияние запаздывания на устойчивость
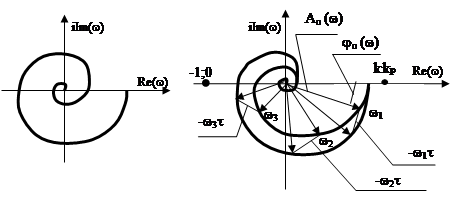 Обычно АФХ разомкнутой системы представляет собой спираль, навивающуюся
на начало координат. Пусть передаточная функция разомкнутой системы содердит
звено запаздывания
Обычно АФХ разомкнутой системы представляет собой спираль, навивающуюся
на начало координат. Пусть передаточная функция разомкнутой системы содердит
звено запаздывания ![]() , где
, где ![]() - передаточная
функция предельной системы, которая не содержит звеньев запаздывания.
- передаточная
функция предельной системы, которая не содержит звеньев запаздывания.
Предположим, что
АФХ разомкнутой системы не охватывает точку (-1;0). Звено запаздывания не
изменит амплитудо-частотную характеристику разомкнутой системы, так как ![]() , а
, а ![]() .
Амплитудо-частотная характеристика разомкнутой системы:
.
Амплитудо-частотная характеристика разомкнутой системы: ![]() .
.
Следовательно,
для получения АФХ разомкнутой системы ![]() необходимо
АФХ предельной системы повернуть на угол
необходимо
АФХ предельной системы повернуть на угол ![]() , то
есть каждую точку АФХ предельной системы
, то
есть каждую точку АФХ предельной системы ![]() повернуть
на угол
повернуть
на угол ![]() , где
, где ![]() -частота
соответствующая точкам АФХ
-частота
соответствующая точкам АФХ ![]() .
.
Очевидно, что
полученная с учетом запаздывания АФХ разомкнутой системы ![]() будет расширяться и может охватить
точку (-1;0), что приведет к неустойчивости замкнутой системы в соответствии с
критерием Найквиста.
будет расширяться и может охватить
точку (-1;0), что приведет к неустойчивости замкнутой системы в соответствии с
критерием Найквиста.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.