 Переходной характеристикой
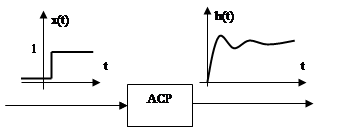
называется реакция системы на единичное скачкообразное возмущение при нулевых
начальных условиях. Переходная характеристика обозначается как h(t). Единичная скачкообразная функция
Переходной характеристикой
называется реакция системы на единичное скачкообразное возмущение при нулевых
начальных условиях. Переходная характеристика обозначается как h(t). Единичная скачкообразная функция 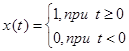 .
Переходная характеристика образует переходный процесс в системе.
.
Переходная характеристика образует переходный процесс в системе.
Переходную характеристику можно получить как решение дифференциального уравнения, описывающего систему при x(t)=1 либо, учитывая определение передаточной функции:
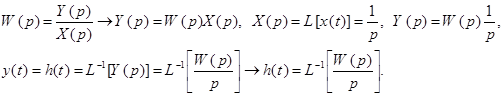
Зная аналитический
вид переходной характеристики и входного возмущающего воздействия можно
определить реакцию системы, т.е. переходный процесс, на входное воздействие
любого вида по формуле Дюамеля: ![]() .
.
Кривой разгона называется реакция системы y(t) на входное воздействие произвольной величины.
Свойства переходной характеристики:
1. Начальное значение переходной характеристики равно конечному значению передаточной функции:
![]() .
.
Пример. Пусть ![]() . Тогда
. Тогда ![]() .
.
2. Конечное значение переходной характеристики равно начальному значению передаточной функции:
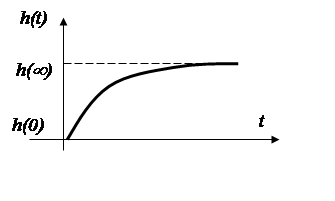
![]()
Пример. Для ![]() и
и ![]() получим:
получим:
![]() .
.
Импульсная характеристика.
Импульсной характеристикой называется реакция системы на единичное импульсное возмущение при нулевых начальных условиях.
Импульсная характеристика обозначается: V(t), ее также называют функцией веса или весовой функцией.
Единичное
импульсное возмущение 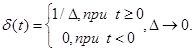
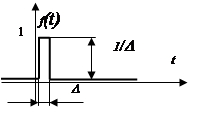 Функция
Функция ![]() называется дельта-функцией Дирака. Она
обладает свойствами:
называется дельта-функцией Дирака. Она
обладает свойствами: ![]() . Последнее свойство легко
проиллюстрировать графически:
. Последнее свойство легко
проиллюстрировать графически: ![]() . Т.е.
. Т.е. ![]() - это такая функция, площадь под
которой равна единице.
- это такая функция, площадь под
которой равна единице.
Импульсную
характеристику можно получить из определения передаточной функции: ![]() , Учитывая, что
, Учитывая, что ![]() ,
тогда
,
тогда ![]() , где
, где ![]() .
Тогда
.
Тогда ![]() .
.
Импульсные характеристики применяются, когда по технологическим соображениям недопустимы большие отклонения регулируемой величины объекта управления.
Частотные характеристики.
Частотные характеристики – это реакция системы на входное воздействие в виде колебаний гармонической формы.
 Пусть на вход системы
подается сигнал гармонической формы:
Пусть на вход системы
подается сигнал гармонической формы:
![]() , где
, где ![]() - амплитуда входных колебаний, w - круговая
частота, рад/с,
- амплитуда входных колебаний, w - круговая
частота, рад/с, ![]() , где Т – период
входных колебаний.
, где Т – период
входных колебаний.
Со временем на выходе системы установятся также колебания гармонической формы, y(t), причем для линейных систем, которые описываются линейным дифференциальным уравнением частота колебаний w не измениться. На выходе системы установятся колебания вида:
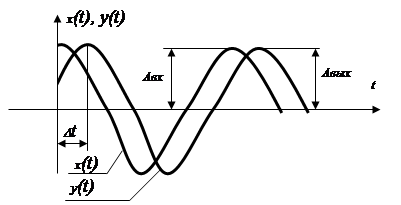
![]() , где
, где ![]() - амплитуда выходных колебаний, j - угол сдвига по
фазе выходных колебаний относительно входных,
- амплитуда выходных колебаний, j - угол сдвига по
фазе выходных колебаний относительно входных, ![]() ,
рад.
,
рад.
Амплитуда выходных
колебаний ![]() зависит от частоты w:
зависит от частоты w:
![]()
Сдвиг фаз j также зависит от частоты.
Для инерционных объектов
управления происходит сдвиг фаз в сторону отставания, т.е. ![]() в данном случае будет иметь
отрицательный знак.
в данном случае будет иметь
отрицательный знак.
Амплитудо-частотной характеристикой (АЧХ) называется зависимость отношения амплитуды выходного сигнала к амплитуде входного от частоты.
![]() .
.
Фазо-частотной
характеристикой (ФЧХ) называется зависимость сдвига
фазы выходных колебаний системы по отношению к входным от частоты. ФЧХ
обозначается: ![]() .
.
Пусть входной гармонический сигнал представлен в комплексном виде:
![]() , тогда выходной сигнал будет
, тогда выходной сигнал будет ![]() .
.
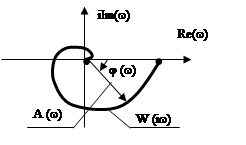 Амплитудо-фазовой
характеристикой (АФХ) называется отношение выходного сигнала ко входному в
комплексном виде:
Амплитудо-фазовой
характеристикой (АФХ) называется отношение выходного сигнала ко входному в
комплексном виде:
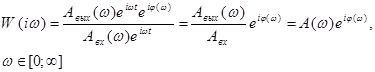 .
.
Очевидно, что
модуль АФХ представляет собой АЧХ ![]() , а аргумент АФХ
является ФЧХ системы
, а аргумент АФХ
является ФЧХ системы ![]() .
.
Обычно график АФХ имеет вид спирали, навивающейся на начало координат.
Сформулируем алгоритм экспериментального получения частотных характеристик:
1. На вход системы необходимо подать сигнал гармонической формы: ![]() .
.
2. Дождаться установления колебаний на выходе системы, т.е. колебаний посточянной формы.
3. Определить амплитуду выходных колебаний ![]() и
точку АЧХ, соответствующую частоте w:
и
точку АЧХ, соответствующую частоте w: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.