Математика \ Математическое описание автоматических систем

Уравнения автоматических систем. Описание систем в пространстве состояний. Динамические характеристики автоматических систем, страница 8

Третья теорема Ляпунова.

Если характеристическое уравнене линеаризованной системы содержит мнимые корни, то об устойчивости реальной нелинейной системы говорить нельзя, так как на установившийся режим влияют отброшенные члены ряда Тейлора.

Корневой критерий устойчивости

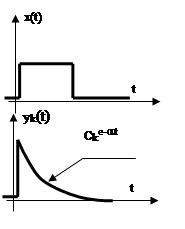Рассмотрим систему после нанесения возмущения, ее выход будет описываться зависимостью , где - корни харакеристического уравнения системы.

1. Пусть для , т.е. все корни характеристического уравнения отрицательные.

Каждая составляющая процесса на выходе системы , где будет стремиться к нулю при . Если все составляющие будут стремиться к нулю, то, очевидно, что выход системы после прекращения возмущения в установившемся режиме равен выходу системы до нанесения возмущения. Значит система будет устойчивой.

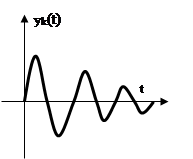2. Пусть для , т.е. корни характеристического уравнения комплексные с отрицательной вещественной частью. Составляющая, соответствующая этому корню будет иметь вид: .При эта составляющая будет стремиться к нулю, так как . Если все остальные составляющие тоже будут стремиться к нулю, т.е. все остальные корни будут иметь отрицательные вещественные части или , то выход системы после прекращения действия возмущения в установившемся режиме будет равен выходу системы до нанесения возмущения. Следовательно, система будет устойчивой.

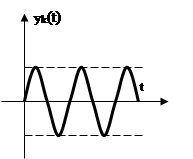
3. Пусть , т.е. корни чисто мнимые. Составляющая, соответствующая этому корню будет иметь вид: . Если все остальные составляющие будут стремиться к нулю при , то, очевидно, что такая система будет находиться на границе устойчивости.

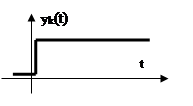4. Пусть , т.е. имеется нулевой полюс. Составляющая, соответствующая этому корню:. Если все остальные составляющие будут стремиться к нулю при , то такая система будет нейтрально устойчивой.

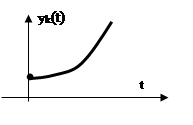5. Пусть , т.е. имеется положительный корень. Составляющая, соответствующая этому корню:. будет неограниченно возрастать при , Даже если все остальные составляющие будут стремиться к нулю при , то выход системы будет неограниченно возрастать, т.е. такая система будет неустойчивой.

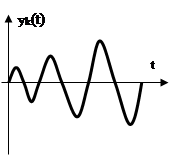6. Пусть , т.е. имеются комплексные корни с положительной вещественной частью. Составляющая, соответствующая этому корню имеет вид: . При будет неограниченно возрастать, так как . Даже если все остальные составляющие будут стремиться к нулю, то выход системы будет неограниченно возрастать при , т.е. такая система будет неустойчивой.

Формулировка корневого критерия устойчивости.

Система будет устойчивой, если вещественные части всех корней характеристического уравнения системы будут отрицательными.

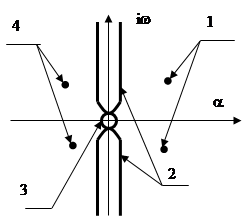
Графически критерий можно интерпритировать следующим образом: для устойчивости системы корни ее характеристического уравнения должны лежать в левой полуплоскости на плоскости корней характеристического уравнения.

Пример 1.

Определить устойчивость системы, которая описывается уравнением:

. Система неустойчива .