Пример.
Найти решение
дифференциального уравнения: ![]() , при условии, что x(t)
– единичное, скачкообразное возмущение, т. е.
, при условии, что x(t)
– единичное, скачкообразное возмущение, т. е. ![]() .
.
Найдем
преобразования Лапласса для дифференциального уравнения: ![]() . Изображение от y(t):
. Изображение от y(t): ![]()
![]() .
.
Передаточные функции.
Общий вид уравнений динамики, описывающих автоматические системы имеет структуру:
![]()
Преобразуем уравнение (1) по Лаплассу. Получим:
![]() , где Y(p)
- изображение функции y(t), X(p) - изображение функции x(t). Y(p)=L[y(t)], X(p)=L[x(t)].
, где Y(p)
- изображение функции y(t), X(p) - изображение функции x(t). Y(p)=L[y(t)], X(p)=L[x(t)].
Преобразуем уравнение (2) – вынесем за скобки Y(p) и X(p). Получим:
![]() .
.
Из уравнения (3) найдем отношение изображений по Лаплассу Y(p) и X(p):
![]() .
.
Передаточной функцией W(p) называют отношение изображений по Лапласу реакции системы y(t) к изображению входного воздействия x(t) при нулевых начальных условиях.
![]()
Пример.
Найти передаточную
функцию дифференциального уравнения ![]() .
.
Преобразуем по
Лапласу это уравнение: ![]() , тогда
, тогда ![]() .
.
Передаточная функция описывает свойства системы аналогично дифференциальному уравнению. Применение передаточной функции для описания динамики систем вызвано преимуществом использования преобразования Лапласса – в этом случае осуществиться переход от дифференциальных уравнений к обычным алгебраическим уравнениям относительно p.
Знаменатель передаточной функции называется характеристическим уравнением системы. Корни знаменателя передаточной функции называются полюсами передаточной функции. Корни числителя передаточной функции называются нулями передаточной функции.
Пример.
![]() . Здесь характеристическое уравнение
будет
. Здесь характеристическое уравнение
будет ![]() . Здесь передаточная функция имет один
полюс
. Здесь передаточная функция имет один
полюс ![]() .
.
Пример.
![]() . Здесь характеристическое уравнение
будет
. Здесь характеристическое уравнение
будет ![]() . Здесь передаточная функция имет два
полюса
. Здесь передаточная функция имет два
полюса ![]() ,
, ![]() ,
один нуль
,
один нуль ![]() .
.
По передаточной функции можно найти реакцию системы, т.е. процесс на выходе y(t).
Из уравнения (5)
можно записать: ![]() . Предположим, что
передаточная функция системы известна и равна W(p). Входное воздействие также известно, и представляет собой единичную
скачкообразную функцию, изображение по Лапласу которой
. Предположим, что
передаточная функция системы известна и равна W(p). Входное воздействие также известно, и представляет собой единичную
скачкообразную функцию, изображение по Лапласу которой ![]() ,
(см. таблицу изображений). Тогда реакция системы y(t) на x(t) будет:
,
(см. таблицу изображений). Тогда реакция системы y(t) на x(t) будет: ![]() .
.
Пример.
Передаточная функция
системы ![]() , входное воздействие – единичное
скачкообразное.
, входное воздействие – единичное
скачкообразное.
 Тогда реакция системы
будет
Тогда реакция системы
будет 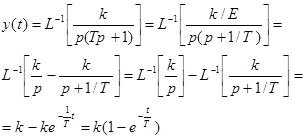
Алгоритм решения дифференциального уравнения динамики.
1. По дифференциальному уравнению при помощи преобразования Лапласса находим передаточную функцию.
2. Находим изображение X(p) входного воздействия на систему x(t) по таблицам изображений.
3. Находим изображение выхода системы: Y(p)=W(p)X(p).
4. Полученное выражение Y(p) преобразуем в сумму простых дробей для нахождения табличного изображения каждой составляющей этой схемы [см. пример выше].
5. По таблицам изображений находим оригиналы каждой составляющей и получаем реакцию системы y(t) на входное воздействие x(t).
Вопросы.
1. В чем состоит преимущество описания систем в пространстве состояний?
2. С какой целью в ТАУ используется преобразование Лапласса?
3. Как получить передаточную функцию из дифференциального уравнения?
4. Что называется передаточной функцией?
5. Для чего используется описание динамики систем в виде передаточной функции?
6. Каково достоинство описания систем с помощью передаточной функции?
7. Что такое нули и полюса передаточной функции?
8. Что представляет собой характеристическое уравнение в ТАУ?
9. Как с помощью передаточной функции определить реакцию системы, т.е. процесс изменения ее выхода на единичное скачкообразное возмущение на входе системы?
10. Как с помощью апарата передаточной функций найти решение дифференциальное уравнение динамики системы?
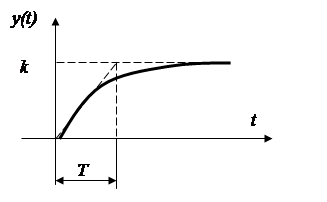
Динамические характеристики автоматических систем
Переходная характеристика.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.