Уравнения автоматических систем. Описание систем в пространстве состояний. Динамические характеристики автоматических систем, страница 5

4.  Определить фазовый сдвиг выходных колебаний относительно входных и вычислить точку ФЧХ, соответствующую частоте w: , где  - временной сдвиг входных и выходных колебаний.

5.  Повторить пункты 1-4 для значений частоты .

6.  Построить графики АЧХ A(w) и ФЧХ j(w) для .

7.  На основании данных АЧХ и ФЧХ построить на комплексной плоскости график АФХ, для , используя полярную систему координат, где модулем вектора служит A(w), а углом его поворота - j(w).

Алгоритм получения частотных характеристик в аналитическом виде.

1.  По дифференциальному уравнению динамики необходимо найти передаточную функцию.

2.  В передаточной функции осуществляется замена: p=iw . В этом случае полученная АФХ будет иметь вид:

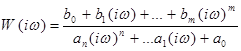
3.  Аналитическую запись АФХ необходимо преобразовать к виду:

.

На комплексной плоскости строиться график АФХ по значениям вещественной и мнимой части АФХ для .

4.  АЧХ будет иметь вид: , ФЧХ: . АФХ будет иметь вид: .

Необходимо отметить, что из-за инерционности в реальных системах при увеличении w всегда будет такая частота w_ср  , при которой система перестает реагировать на входное возмущение гармонической формы. w_ср  называется частотой среза.

В реальных условиях амплитуда выходного сигнала с увеличением w  никогда не возрастает неограничено, т.е. для аналитического вида АФХ  всегда m£n. Если от АФХ перейти к передаточной функции, а затем к дифференциальному уравнению, то условие m£n будет означать, что инерционность выхода объекта управления всегда бодьше, чем инерционность на входе. Такое условие проистекает из физических свойств динамических систем.

Вопросы.

1.  Что называется переходной характеристикой системы, в чем ее отличие от кривой разгона?

2.  Как по передаточной функции найти аналитический видж переходной характеристики?

3.  Каковы основные свойства дельта-функции Дирака ?

4.  Что называется импульсной характеристикой, в каких случаях она используется для получения динамических характеристик объектов управления? Как получить аналитичский вид импульсной характеристики?

5.  Что представляет собой АЧХ? ФЧХ?

6.  Какова связь между АФХ, АЧХ и ФЧХ?

7.  Как получить аналитический вид АФХ?

8.  Что такое частота среза?

9.  Как определяется круговая частота w, какова ее размерность?

10.  Как зная АЧХ и ФЧХ системы построить АФХ?

Д/З. Дана передаточная функция . Найти дифференциальное уравнение для этой передаточной функции и рассчитать h(t) по формуле: 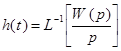 для случаев:

1.

2.

3.

4. , т.е.

5. .

Ключ к решению: таблица изображений, п. 4,8,9,10,11.

Элементарные динамические звенья.

Элементарным звеном называется модель, связывающая входной и выходной сигнал абстрактной системы. К элементарным относят динамические звенья, которые описываются дифференциальным уравнением не выше II-го порядка.

Пропорциональное звено.

Пропорциональным звеном называется такое звено, выходной сигнал которого пропорционален входному сигналу.

Уравнение пропорционального звена: , где k –коэффициент передачи звена. Пропорциональное звено называется также безинерционным, усилительным звеном.

Передаточную функцию звена найдем из его уравнения: .

Переходная характеристика звена: , при .

Импульсная характеристика звена: .

АФХ: ,

АЧХ: ,

ФЧХ: .

Вывод:  по виду АФХ очевидно, что входной сигнал гармонической формы при прохождении через пропорциональное звено усиливается по амплитуде в  k раз, а сдвига по фазе не происходит.

Апериодическое звено I-го порядка.

Апериодическим звеном называется такое звено, динамика которого описывается дифференциальным уравнением:

, где k – коэффициент передачи, T – постоянная времени [с].

Апериодическое звено называется также инерционным звеном I-го порядка.

Передаточная функция: .