Уравнения автоматических систем. Описание систем в пространстве состояний. Динамические характеристики автоматических систем, страница 2

где - вектор переменных состояния;  - вектор управляющих воздействий; А и В – матрицы коэффициентов.

,  ,   ,  ,   .

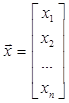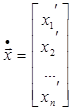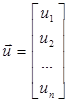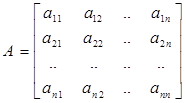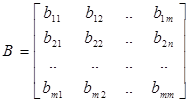Уравнение (2) описывает только лишь динамику системы. Для того, чтобы получить значение выходных параметров системы необходимо найти значение вектора выходов . В матричной форме записи:

, где  C и D  - матрицы, . Таким образом в пространстве состояний описание системы имеет вид:

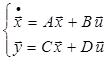
Рассмотрим пример перехода от описания системы линейных дифференциальных уравнений к описанию системы в пространстве состояний.

Пусть система описывается дифференциальным уравнением: . Обозначим переменные состояния: , , . Тогда :

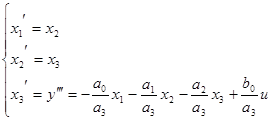 или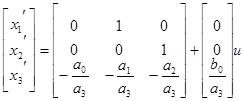

Так как система имеет один выход, то уравнение (3) будет иметь вид:

.

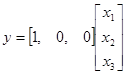Достоинства описания систем в пространстве состояний:

1.  Универсальное описание различных систем.

2.  Возможность универсального решения задач многомерными системами, содержащими несколько входов и выходов.

Недостатки:

1.  Недостаточная наглядность описания.

2.  Проблемы вычислительного характера.

Преобразование Лапласса.

В ТАУ широко применяются методы операционного исчисления, в основе которых лежит преобразование Лапласса. Оно преобразует функцию вещественной переменной в функцию комплексной переменной F(p) по формуле: . Функция f(t) называется оригиналом, F(p) – изображением по Лаплассу. Обозначают:

 и , где L – орератор Лапласса.

Применение преобразования Лапласса облегчает решение дифференциального уравнения динамики, так как при этом  дифференциальные уравнения заменяются алгебраическими уравнениями относительно р.

Основные свойства преобразования Лапласса:

1.  Свойство линейности.

.

Пример.

. Тогда , где Y(p) – изображение функции y(t),  - изображения функциий .

2.  Дифференцирование оригинала.

.

Пример.

.

Преобразуя по Лаплассу, получим: .

3.  Интегрирование орогинала.

.

Пример.

, тогда .

4.  Теорема запаздывания.

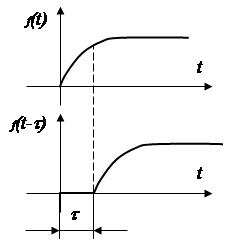
, где t - положительное число.

Проиллюстрируем функцию запаздывания графически. При  функция .

Пример.

, тогда .

Пример.

, тогда .

Таблица оригиналов и изображений

№	Оригинал f(t)	График f(t)	Изображение
1
2	, где. называется дельта-функцией Дирака. .
3		f(t)
4		f(t)
5		t   f(t)
6		f(t)   t
7		t   f(t)
8		f(t)
9		f(t)   t
10		f(t)
11		f(t)