Уравнения автоматических систем. Описание систем в пространстве состояний. Динамические характеристики автоматических систем, страница 7

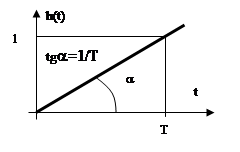
Иногда уравнение звена записывается в виде: , где - приведенная скорость звена. Коэффициент  равен скорости изменения выхода при подаче единичного скачкообразного возмущения на вход.

=.

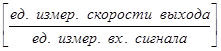Передаточная функция: .

Переходная характеристика. .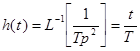

Постоянная времени интегрирования представляет собой  промежуток времени, за который выход звена достигнет 1, при подаче единичного скачкообразного возмущения на вход.

Импульсная характеристика:

.

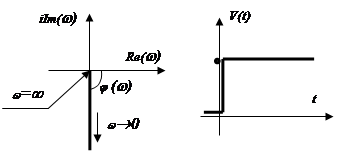
АФХ: .

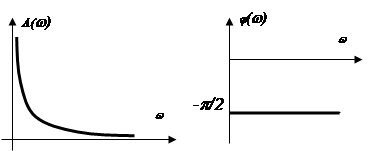
АЧХ: .

ФЧХ: .

1/T

      Идеальное дифференцирующее звено

Идеальным дифференцирующим звеном называется такое звено, свойства которого описываются уравнением:

  

Передаточная функция: .

Переходная характеристика. .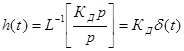

Импульсная характеристика:

.

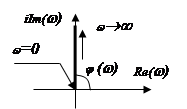
АФХ: .

АЧХ: .

ФЧХ: .

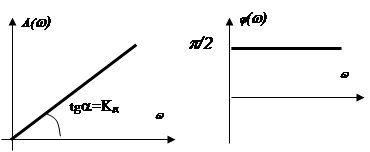
Вывод. Илеальное дифференцирующее звено является идеальной моделью, что на прктике возможно лишь на  на некоторой степени приближения. Отметим, что ????????? на выходе звена будет опережать по фазе входной сигнал  на  рад.

      Реальное дифференцирующее звено

Реальным дифференцирующим звеном называется такое звено, динамика которых описывается дифференциальным уравнением:

   , где  - коэффициент передачи реального дифференцирующего звена,  - постоянная времени.

Передаточная функция: .

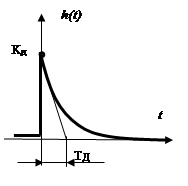
Переходная характеристика. .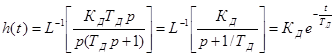

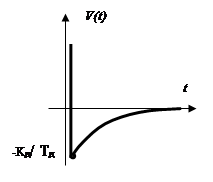Найдем переходную характеристику, решив дифференциальное уравнение звена. Его решение будет иметь вид: , учитывая, что , найдем постоянную С из свойств переходной характеристики:

, тогда

Импульсная характеристика:

.

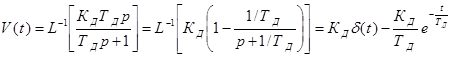АФХ: .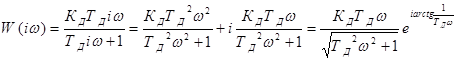

АЧХ: .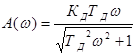

ФЧХ: .

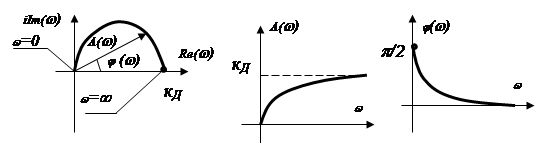
Вывод. Выходной сигнал опережает по фазе входной гармонический сигнал. Переходная характеристика , т.е. возвращается на первоначальный ее уровень до нанесения возмущения

      Звено запаздывания

Звеном запаздывания называется такое звено, свойства которого описывается уравнением:

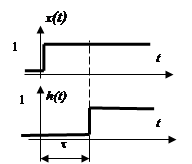
   , где  - величина запаздывания, [с]. Всегда >0.

Передаточная функция: .

Переходная характеристика. .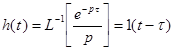

Импульсная характеристика:

.

АФХ: .

АЧХ: .

ФЧХ: .

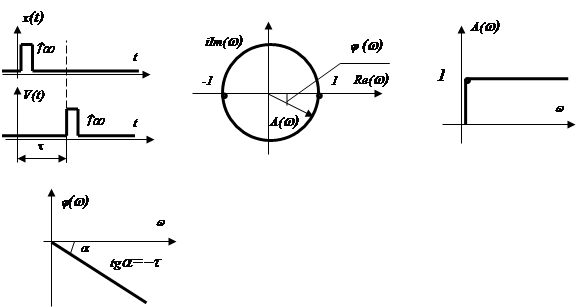
Вывод. Гармонический сигнал при прохождении через звено запаздывания не искажается по амплитуде, а сдвиг по фазе идет в сторону отставания.

Устойчивость систем управления.

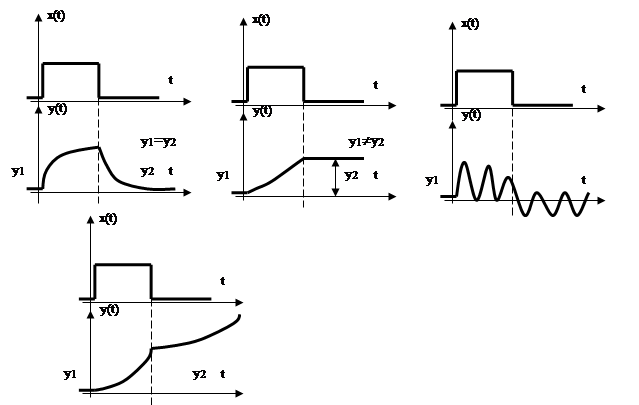
Устойчивой называется такая система, в которой при нанесении возмущения  и прекращения его действия выходная величина системы в установившемся режиме будет равна ее значению до нанесения возмущения.

Нейтрально устойчивой называется такая система, в которой при нанесении возмущения и прекращении его действия выходная величина системы в установившемся режиме будет отличаться от ее значения до нанесения возмущения.

Системой на границе устойчивости называется такая система, в которой  при нанесении возмущения и прекращении его действия выходная величина системы совершает гармонические колебания.

Неустойчивой называется такая система, в которой при нанесении возмущения и прекращении его действия выходная величина системы будет неограниченно возрастать.

Реальные АСР должны быть устойчивыми. Учитывая тот факт, что реальные АСР практически всегда являются нелинейными в отличие от из линеаризованных моделей, необходимо выяснить связь между устойчивостью реальной нелинейной АСР и ее линеаризованной моделью.

Первая теорема Ляпунова.

Если все корни характеристического уравнения линеаризованной системы являются отрицательными: , то реальная нелинейная система будет устойчивой, т.е. если линейная модель системы будет устойчива, то добавлением отброшенных членов ряда Тейлора ее невозможно превратить в неустойчивую.

Вторая теорема Ляпунова.

Если хотя бы один корень характеристического уравнения линеаризованной системы , то реальная нелинейная система будет неустойчивой, т.е. если линейная модель системы будет неустойчива, то добавлением отброшенных членов ряда Тейлора ее невозможно превратить в устойчивую.