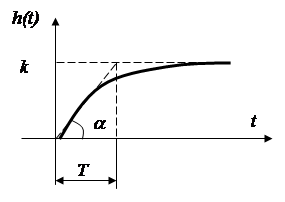
 Переходная
характеристика.
Переходная
характеристика.
Характеристическое
уравнение имеет вид: ![]() , полюс которого
, полюс которого ![]() . Решение дифференциального уравнения
имеет вид:
. Решение дифференциального уравнения
имеет вид: ![]() , учитывая, что
, учитывая, что ![]() ,
получим
,
получим ![]() . Тогда
. Тогда ![]() .
.
Определим величину
проекции касательной к ![]() в момент времени
в момент времени ![]() на ось t:
на ось t:
![]() .
.
Проекция на ось t будет: 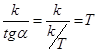 .
.
Импульсная
характеристика: 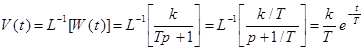 .
.
АФХ: ![]() , т.к.
, т.к. ![]()
АЧХ: ![]() ,
,
ФЧХ: ![]() .
.
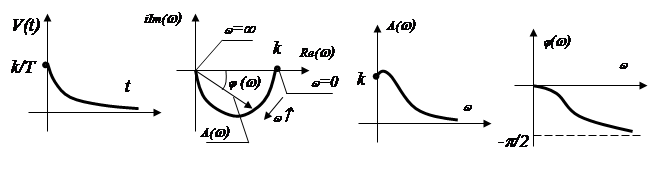 |
Вывод.
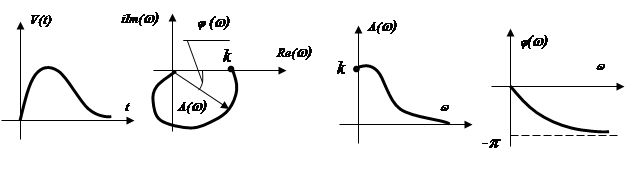
По АЧХ видно, что при увеличенни частоты w входного сигнала уменьшается амплитуда сигнала на выходе звена. Таким образом звено уменьшает амплитуду высокочастотных сигналов. Говорят, что происходит демпфирование – сглаживание сигналов по амплитуде.
По ФЧХ видно, что
выходной сигнал сдвигается по фазе в сторону отставания от входного сигнала,
т.к. ![]() .
.
Д/З. Построить АФХ звена с передаточной функцией вида:
1. ![]() ; 2.
; 2. ![]() ;
3.
;
3. ![]() .
.
Сделать вывод о влиянии постоянной времени звена на вид АФХ.
Пример. Определить
параметры звена с передаточной функцией: ![]() .
.
![]() .
.
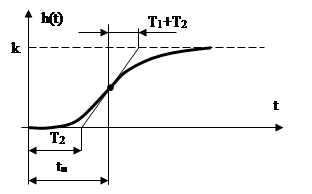
Апериодическое звено II-го порядка.
Апериодическим звеном II-го порядка называется такое звено, динамика которого описывается дифференциальным уравнением:
![]() , вслучае, когда
, вслучае, когда
![]() .
.
Здесь ![]() - постоянные времени, k-
коэффициент передачи звена.
- постоянные времени, k-
коэффициент передачи звена.
Передаточная
функция: ![]() .
.
Учитывая, что ![]() , то передаточную функцию (2) можно
представить в виде:
, то передаточную функцию (2) можно
представить в виде:
![]()
В передаточной
функции (3) ограничения на ![]() не накладываются,
т.е. передаточная функция (3) включает в себя условие (1).
не накладываются,
т.е. передаточная функция (3) включает в себя условие (1).
Переходная характеристика. Найдем переходную характеристику с помощью преобразований Лапласса:
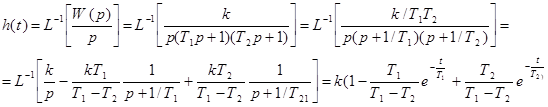 .
.
|
Импульсная характеристика:
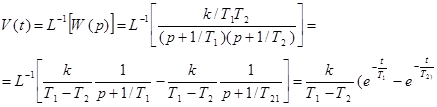 .
.
АФХ: 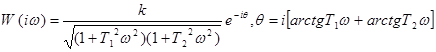
АЧХ: 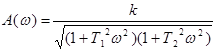 .
.
ФЧХ: ![]() .
.
Консервативное звено.
Консервативным звеном называется такое динамическое звено, свойства которого описывается дифференциальным уравнением:
![]()
![]() ,
,
![]() где k – коэффициент передачи, Т - постоянная времени.
где k – коэффициент передачи, Т - постоянная времени.
![]() Передаточная функция:
Передаточная функция: ![]() .
.
![]() Переходная характеристика. Найдем переходную характеристику с помощью
преобразований Лапласса:
Переходная характеристика. Найдем переходную характеристику с помощью
преобразований Лапласса:
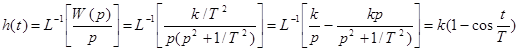 .
.
Импульсная характеристика:
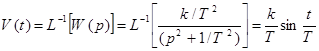 .
.
АФХ: ![]()
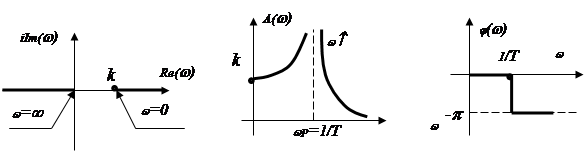 АЧХ:
АЧХ: ![]() .
.
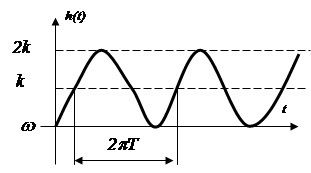 ФЧХ:
ФЧХ: 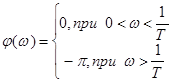 , где Т – постоянная времени
звена.
, где Т – постоянная времени
звена.
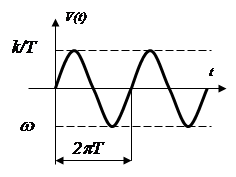
Вывод. При
частоте входных колебаний ![]() за счет явления
резонанса амплитуда выходных колебаний будет неограничено возрастать, что видно
из графика АФХ
за счет явления
резонанса амплитуда выходных колебаний будет неограничено возрастать, что видно
из графика АФХ ![]()
![]() .
.
Колебательное звено.
Колебательным звеном называется такое динамическое звено, свойства которого описываются дифференциальным уравнением:
![]()
![]() , когда
, когда ![]() где
где ![]() ,
, ![]() – постоянные времени, k - коэффициент
передачи.
– постоянные времени, k - коэффициент
передачи.
![]() Передаточная функция:
Передаточная функция: ![]() .
.
![]() Рассмотрим варианты отношения
Рассмотрим варианты отношения ![]() .
.
![]() 1. Пусть
1. Пусть ![]() . Характеристическое уравнение будет
иметь вид:
. Характеристическое уравнение будет
иметь вид: ![]() , тогда
, тогда
![]()
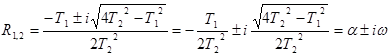 ,
причем
,
причем ![]() .
.
![]() Тогда решение дифференциального
ураавнения будет иметь вид:
Тогда решение дифференциального
ураавнения будет иметь вид:
![]()
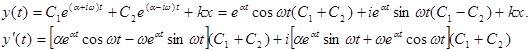
![]() Из начального условия
Из начального условия ![]() найдем:
найдем:
![]()
![]()
Тогда переходная
характеристика имеет вид: ![]() .
.
Очевидно, что ![]() можно найти с помощью преобразований
Лапласса.
можно найти с помощью преобразований
Лапласса.![]()
Импульсную
характеристику можно найти так: 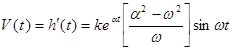 .
.
2. Пусть ![]() . Тогда дискриминант
характеристического уравнения
. Тогда дискриминант
характеристического уравнения ![]() .
. ![]() . Решение дифференциального уравнения
будет иметь вид:
. Решение дифференциального уравнения
будет иметь вид:
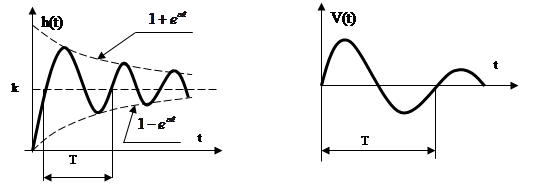
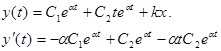 .
.
Из начальных
условий ![]() найдем
найдем ![]() .
.
Тогда переходная
характеристика: ![]() . Аналогично можно найти
. Аналогично можно найти ![]() используя преобразование Лапласа.
используя преобразование Лапласа.
3. Пусть ![]() . Тогда колебательное звено выглядит
как апериодическое звено II- го порядка.
. Тогда колебательное звено выглядит
как апериодическое звено II- го порядка.
4. Пусть ![]() , т.е.
, т.е. ![]() .
Тогда колебательное звено выглядит как апериодическое звено I- го порядка.
.
Тогда колебательное звено выглядит как апериодическое звено I- го порядка.
5. Пусть ![]() , т.е.
, т.е. ![]() .
Тогда колебательное звено вырождается в консервативное звено.
.
Тогда колебательное звено вырождается в консервативное звено.
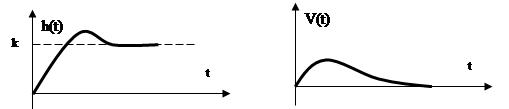
АФХ: 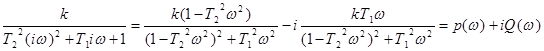
АЧХ: 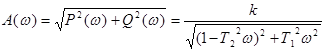
![]() ФЧХ:
ФЧХ: ![]() .
.
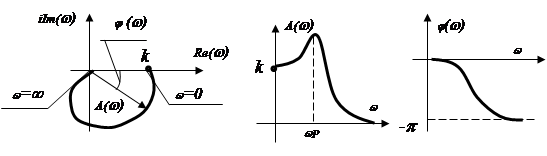
Вывод: при частоте входных колебаний ![]() будет наблюдаться резонансное
увеличение амплитуды выходных колебаний.
будет наблюдаться резонансное
увеличение амплитуды выходных колебаний.
Интегрирующее звено.
Интегрирующим звеном называется такое динамическое звено, свойства которого описываются уравнением:
![]()
![]() ,
или
,
или ![]() , где Т - постоянная времени интегрирования, [с].
, где Т - постоянная времени интегрирования, [с].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.