Итак, увеличение запаздывания в системе негативно влияет на ее устойчивость, вплоть до выхода системы на границу устойчивости и перехода в неустойчивое состояние. При пректических расчетах выход системы на границы устойчивости можно определить следующим образом.
1. Необходимо провести окружность единичного радиуса с центром в начале координат.
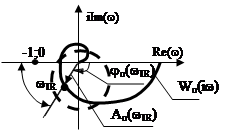 Определить точку пересечения этой окружности с АФХ предельной системы
Определить точку пересечения этой окружности с АФХ предельной системы ![]() и найти
соответствующую ей частоту
и найти
соответствующую ей частоту ![]() .
.
2. Определить
угол ![]() между отрицательной вещественной
полуосью и прямой и прямой, проходящей через начало координат и точку,
соответствующую
между отрицательной вещественной
полуосью и прямой и прямой, проходящей через начало координат и точку,
соответствующую ![]() .
.
3. При
выполнении равенства ![]() , где
, где ![]() -
величина запаздывания. Замкнутая система будет находиться на границе
устойчивости, так как АФХ разомкнутой системы будет проходить через точку
(-1;0).
-
величина запаздывания. Замкнутая система будет находиться на границе
устойчивости, так как АФХ разомкнутой системы будет проходить через точку
(-1;0).
4. Если ![]() , то замкнутая система будет
устойчивой, если же
, то замкнутая система будет
устойчивой, если же ![]() , то система в замкнутом
состоянии будет неустойчивой, так как АФХ разомкнутой системы будет охватывать
точку (-1;0).
, то система в замкнутом
состоянии будет неустойчивой, так как АФХ разомкнутой системы будет охватывать
точку (-1;0).
Аналитически выход системы можно записать так:
Примечание.
Запаздывание
сдвигает выходной сигнал в сторону отставания по фазе относительно входного
сигнала, так как при последовательном соединении звеньев, результирующая ФЧХ
соединения: ![]() , где
, где ![]() -
ФЧХ звена запаздывания. Такой сдвиг по фазе в сторону отставания отрицательно
влияет на устойчивость системы, следовательно любые элементы АСР, которые
сдвигают выходной сигнал в сторону отставания по фазе будут негативно влиять на
устойчивость системы.
-
ФЧХ звена запаздывания. Такой сдвиг по фазе в сторону отставания отрицательно
влияет на устойчивость системы, следовательно любые элементы АСР, которые
сдвигают выходной сигнал в сторону отставания по фазе будут негативно влиять на
устойчивость системы.
Выделение областей устойчивости
Рассмотрим
метод D-разбиения по одному параметру для выделения облатей этого параметра,
при котором система будет устойчива. Пусть характеристическое уравнение системы
имеет вид: ![]() .
.
Предположим, что
исследуемый параметр ![]() , входит в характеристическое
уравнение, тогда оно имеет вид:
, входит в характеристическое
уравнение, тогда оно имеет вид: ![]() . Отсюда можно
выразить параметр
. Отсюда можно
выразить параметр ![]() :
: ![]() .
Сделав замену
.
Сделав замену ![]() , получим:
, получим: ![]() . Полученная кривая называется кривой D-разбиения,
она представляет собой границу перехода левых корней характеристического
уравнения в правые и наоборот. Кривая D-разбиения делит всю комплексную плоскость на
несколько областей. Для того, чтобы определить области устойчивости, необходимо
вдоль кривой D-разбиения нанести с левой стороны штриховку при
возрастании частоты
. Полученная кривая называется кривой D-разбиения,
она представляет собой границу перехода левых корней характеристического
уравнения в правые и наоборот. Кривая D-разбиения делит всю комплексную плоскость на
несколько областей. Для того, чтобы определить области устойчивости, необходимо
вдоль кривой D-разбиения нанести с левой стороны штриховку при
возрастании частоты ![]() от
от ![]() до
до
![]() . Область устойчивости можно определить
как область с максимальным числом штриховок или же, проверив устойчивость
системы для точки внутри этой области.
. Область устойчивости можно определить
как область с максимальным числом штриховок или же, проверив устойчивость
системы для точки внутри этой области.
Пример 1.
Определить область устойчивости кривой D-разбиения, следующего вида:
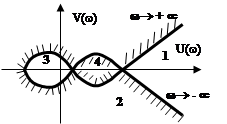 Нанесем штриховку по левую сторону кривой D-разбиения для частоты
Нанесем штриховку по левую сторону кривой D-разбиения для частоты ![]() от
от ![]() до
до ![]() .
Очевидно, что для четырех областей, на которые делится комплексная плоскость,
областью устойчивости будет область 4. Следовательно, для установившейся
системы параметр R должен находиться в области 4.
.
Очевидно, что для четырех областей, на которые делится комплексная плоскость,
областью устойчивости будет область 4. Следовательно, для установившейся
системы параметр R должен находиться в области 4.
Пример 2.
Определить
область значений коэффициента передачи регулятора ![]() ,
при котором замкнутая система будет устойчива.
,
при котором замкнутая система будет устойчива.
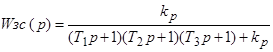 . Из характеристического уравнения
выразим
. Из характеристического уравнения
выразим ![]() и сделаем замену
и сделаем замену ![]() .
.
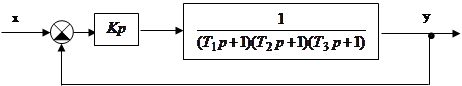
![]() .
.
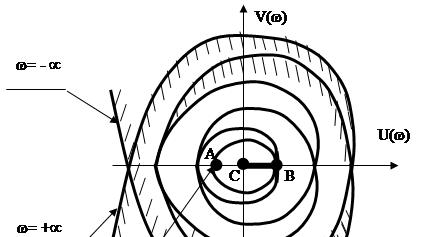
Очевидно, областью устойчивости будет область 3.
Точкам А, В
будет соответствовать частота ![]() .
.
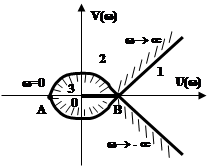
![]() , следовательно
, следовательно
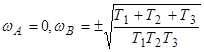 .
.
![]() Так как коэффициент передачи
Так как коэффициент передачи ![]() представляет
вещественное положительное число, то областью устойчивости системы будет
отрезок ОВ,
представляет
вещественное положительное число, то областью устойчивости системы будет
отрезок ОВ, 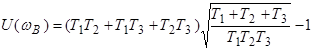 , т.е.
, т.е. ![]()
Пример 3.
Определить область параметров регулятора, при которых система будет устойчивой.
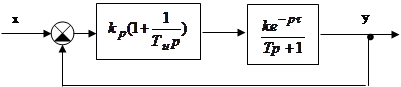 |
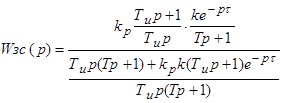 .
.
Характеристическое
уравнение: ![]() . Выделим параметры
. Выделим параметры ![]() и
и ![]() ,
разделив уравнение на
,
разделив уравнение на ![]() .
.
![]() . Подставляем
. Подставляем ![]() :
:
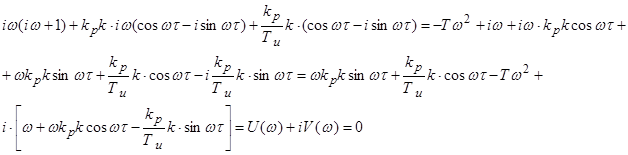
Выразим ![]() и
и ![]() через
w, приравняв к нулю
через
w, приравняв к нулю ![]() .
.
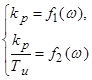 .
.
Так как ![]() , то и
, то и ![]() . В точке
. В точке ![]() ,
, ![]() .
.
Система устойчива, следовательно область устойчивости системы будет следующей:
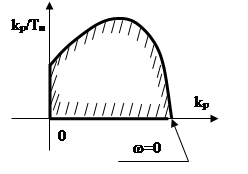
Пример 4.
Определить
область устойчивости системы для коэффициета передачи регулятора ![]() .
.
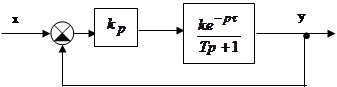 |
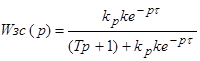
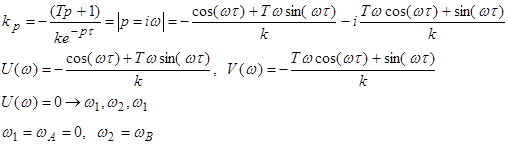
Система будет
устойчивой для ![]()
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.