Образование чертежа. Свойства прямоугольного проецирования. Способы дополнения однопроекционного изображения

расположена дальше от плоскости проекций П¹, значит относительно П¹ точка М видима, а точка N – невидима.

II)  Линия

9)  Классификация линий

9.1. Линия – это множество всех последовательных положений движущейся точки.

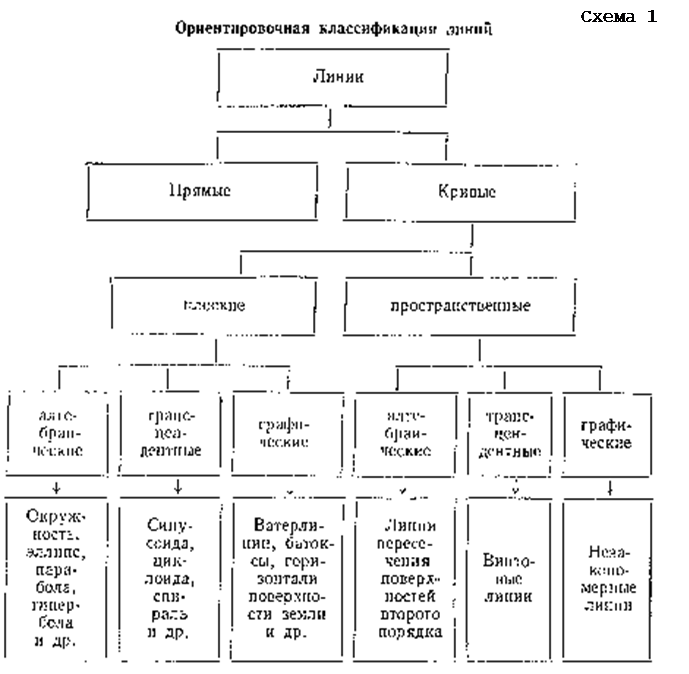9.2. В зависимости от формы и способа образования линии можно разделить на группы по схеме 1.

9.3. Прямая – разновидность линии, которая получается, когда движущаяся точка не изменяет направления своего движения.

9.4. Кривая - разновидность линии, которая получается, когда движущаяся точка изменяет направление своего движения.

9.5. Плоские линии – линии, все точки которых принадлежат одной плоскости.

9.6. Пространственные линии – линии, все точки которых не  принадлежат одной плоскости.

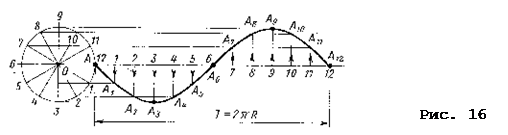
9.7. Алгебраические линии – линии, которые могут быть заданы алгебраическим уравнением, то есть уравнением, в котором общая часть приведена к виду многочлена, целого относительно текущих координат.

9.8. Порядком кривой называют большую степень ее уравнения.

9.9. Графические линии – линии, которые обычно задаются своими проекциями на чертеже.

9.10 Винтовые линии – пространственные линии, получающиеся в результате двойного равномерного движения точки, вращения вокруг оси и поступательного движения вдоль прямой, вращающейся вокруг той же оси.

9.11. Линии могут быть заданы аналитически, то есть уравнением или графически, то есть чертежом.

10)  Алгебраические линии

10.1. Окружность  - плоская замкнутая кривая, все точки которой одинаково удалены от ее центра.

10.2. Эллипс - плоская замкнутая кривая, сумма расстояний от каждой точки которой до двух определенных точек – фокусов – есть величина постоянная.

Существует несколько способов построения эллипса. Например, построение эллипса по заданным осям (рис. 13):

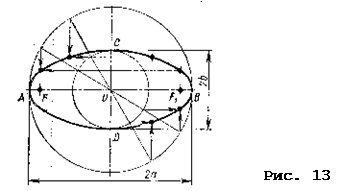Из центра О проводим две концентрические окружности диаметром АВ И СD, равными заданным осям эллипса. Из точки О проводим пучок лучей. Из точек пересечения лучей с окружностями проводим прямые, параллельные осям эллипса, до их взаимного пересечения. Полученные точки принадлежат искомому эллипсу. Эти точки соединяют тонкой линией (обычно от руки). Эллипс применяется для исследования различных движений, например, электронов вокруг ядра, планет в солнечной системе и так далее.

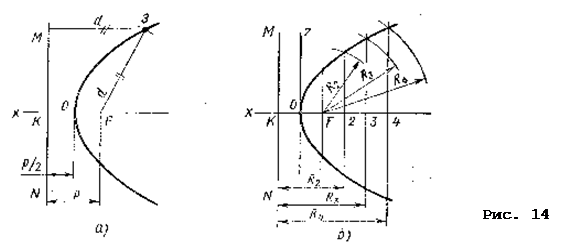
10.3. Парабола – плоская незамкнутая кривая, каждая точка которой равноудалена от прямой MN, называемой директрисой (направляющей), и от точки F – фокуса, расположенного на оси ее симметрии (рис. 14а). Точку О пересечения оси симметрии с параболой называют вершиной, а расстояние KF параметром p – параболы. Известны насколько способов построения параболы, один из них – построение по заданной величине ее параметра:

Проводим две взаимно перпендикулярные прямые – ость x и директрису MN параболы (рис. 14б). От точки К их пересечения откладываем величину параметра и получаем фокус F параболы. Разделив отрезок KF пополам, получаем вершину О параболы. Затем проводим прямые, параллельные директрисе, на произвольных расстояниях от нее. Из фокуса F соответствующими радиус-векторами, равными удалению проведенных прямых от директрисы, например R₂ = K2; R₃ = K3; …, делаем засечки на этих прямых и получаем точки искомой параболы.

11) Трансцендентные линии

11.1. Эвольвентой (разверткой) некоторой плоской линии называется новая плоская кривая, получающаяся в результате двойного равномерного  движения любой точки заданной линии – вращения вокруг некоторого перемещающегося центра и удаления от него (рис. 15).

11.2. Синусоида – плоская кривая, получающаяся в результате двойного равонмерного движения точки – поступательного и возвратно – поступательного, в направлении, перепендикулярном к первому (рис. 16).

III) Прямая

12) Задание и изображение прямой

12.1. Известно, что две точки определяют прямую. Следовательно, для того чтобы задать прямую, необходимо и достаточно задать две ее  точки.

12.2. Образование комплексного чертежа прямой аналогично (рис. 17) образованию комплексного чертежа точки. Для изображения прямой на чертеже необходимо иметь проекции определяющих ее точек, например А и В на рис. 17.

13) Положение прямой относительно плоскостей проекций

13.1. Прямая относительно плоскостей проекций может занимать различные положения и соответственно называться прямой общего положения, прямой уровня и проецирующей прямой.

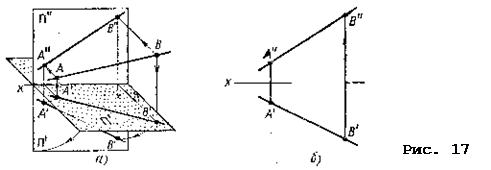
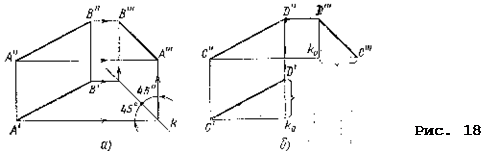
13.2. Прямыми общего положения называются прямые, не параллельные ни одной из плоскостей проекций (рис. 17, 18).

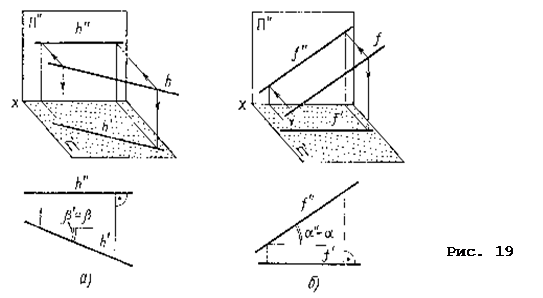
13.3. Прямыми уровня называют прямые, параллельные одной из плоскости проекций (рис. 19).

13.4. Прямые уровня носят различные названия в зависимости от того, какой