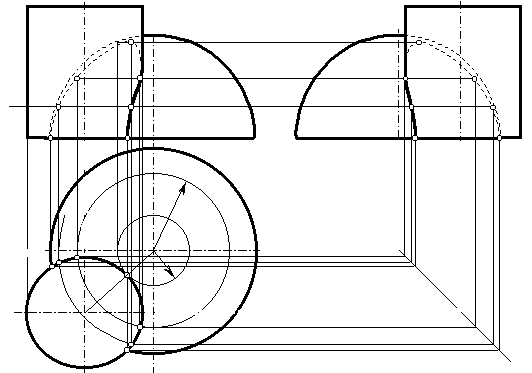
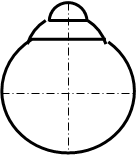
Пример. Построить линию пересечения поверхностей способом секущих плоскостей (рис.87).
Построение осуществляется по заданному алгоритму
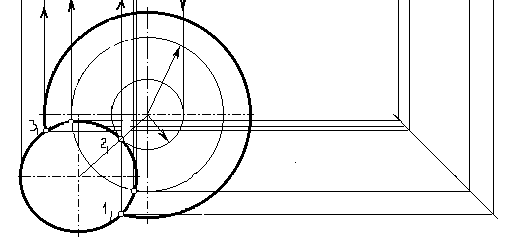
1. Опорные точки 1 и 2 определены на горизонтальной проекции, так как они находятся на пересечении заданных очерков полусферы и цилиндра.
2. Определяем фронтальную проекцию точек 1 и 2, проведя линии связи до изображения основания, так как эти точки располагаются на основании фигур.
3. Наиболее высокой точкой, принадлежащей линии пересечения поверхностей, является точка 2. Вначале определяется ее горизонтальная проекция, а затем достраивается фронтальная с помощью линий связи (рис. 87).
 |
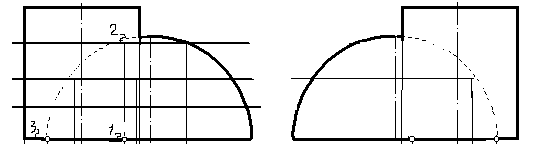 |
 |
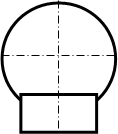
4. Определяем расположение промежуточных точек, принадлежащих линии пересечения поверхностей. Для этого выбираем положение вспомогательных секущих плоскостей в промежутке между опорными точками 1, 2 и 3. Секущие плоскости являются горизонтальными и на фронтальной проекции отображаются в виде прямой линии. На горизонтальной проекции будут отображаться в натуральную величину фигуры сечения тел принятыми плоскостями.
5. Строим фигуры сечения заданными горизонтальными плоскостями на горизонтальной проекции. Фигура сечения полусферы является окружностью, радиус которой равен расстоянию от осевой линии до очерка (на фронтальной проекции). Фигура сечения цилиндра совпадает с его очерком на горизонтальной проекции.
6. Пересечение контуров построенных фигур сечения позволяет определить горизонтальные проекции точек, принадлежащих линии пересечения поверхностей. Фронтальные проекции этих точек строятся с помощью линий связи, проведенных с горизонтальной проекции. Причем, линии связи доводятся до соответствующей секущей плоскости.
7. Профильные проекции точек находятся с помощью линий связи, проведенных соответственно с горизонтальной и фронтальной проекций. Построенные точки одновременно принадлежат каждому из геометрических тел и непосредственно самой линии пересечения поверхностей.
8. Изображение линии пересечения производится после того, как построено достаточное для понимания ее формы количество точек. Соединяя последовательно точки между собой, следует принимать во внимание видимость линии пересечения. Сплошной основной линией показывается видимая часть кривой, а штриховой более тонкой линией отмечается ее невидимая часть (рис. 88).
11. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ СПОСОБОМ КОНЦЕНТРИЧЕСКИХ СФЕР
Для построения точек, принадлежащих линии пересечения поверхностей вращения, используется способ концентрических сфер. Данный способ применяют в тех случаях, когда оси поверхностей вращения пересекаются и расположены параллельно какой-либо плоскости проекций (поверхности имеют общую плоскость симметрии). Для построения линии пересечения подобным способом достаточно одной проекции и соблюдения ряда условий применения указанного способа.
Условия применения способа.
1. Пересекающиеся поверхности должны быть телами вращения.
2. Оси симметрии геометрических тел должны пересекаться.
3. Оси симметрии должны быть параллельны одной и той же плоскости проекций.
 |
|||||
 |
|||||
 |
|||||
Рис. 89
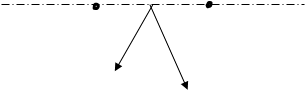
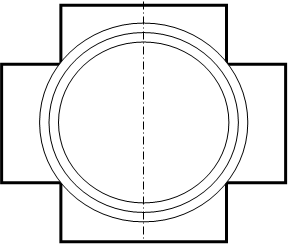
Соосные поверхности пересекаются друг с другом по окружности, проецирующейся на плоскость проекций в виде отрезков прямых (рис.90). Это свойство применяется для данного способа. Сфера пересекает одновременно оба геометрических тела. Полученные при этом фигуры сечения, спроецированные в отрезок прямой, пересекаются и определяют искомые точки.
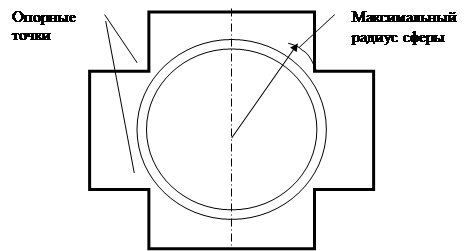
Самая глубокая точка находится с использованием минимального радиуса, являющегося вписанной сферой в наиболее крупное геометрическое тело. Максимальный радиус является расстоянием от точки пересечения осевых линий до точки, расположенной на пересечении контуров заданных геометрических тел (рис. 91).
Алгоритм построения линии пересечения поверхностей способом вспомогательных концентрических сфер
|
№ |
Осуществляемая деятельность |
|
1 |
Анализ изображения на соответствие условиям применения способа |
|
2 |
Определение опорных точек, находящихся на пересечении очерков заданных поверхностей |
|
3 |
Определение центра О для изображения сфер, находящегося на пересечении осевых линий |
|
4 |
Определение максимального радиуса сферы, как наибольшего расстояния от центра О до наиболее удаленной опорной точки, лежащей на пересечении очерков поверхностей |
|
5 |
Определение минимального радиуса сферы, как радиуса вписанной окружности в наиболее крупное по размеру геометрическое тело. Построение наиболее глубоко удаленной точки, принадлежащей линии пересечения поверхностей |
|
6 |
Построение промежуточных точек с использованием промежуточных сфер, радиус которых должен быть меньше максимального радиуса и больше минимального |
|
7 |
Изображение линии пересечения поверхностей, соединяя последовательно построенные точки с помощью лекала |
Пример. Построить линию пересечения двух поверхностей вращения по заданной проекции (рис. 91).
 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1
 |
|||
![]()
![]()
![]()

![]() 2
2
 |
|||
 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1
![]()
![]() 2
2
Рис. 90
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.