Построение линии пересечения поверхностей способом секущих плоскостей. Построение линии пересечения поверхностей способом концентрических сфер, страница 2

Построение осуществляется по заданному алгоритму.

1.  Анализируем графическое условие задачи. Для построения линии пересечения поверхностей воспользуемся методом концентрических сфер, так как форма и расположение геометрических тел соответствуют требуемым  условиям применения метода.

2.  Находим опорные точки  на пересечении очерков двух тел (точки 1 и 2). Они позволяют определить начало и конец линии пересечения.

3.  Находим точку О   на  пересечении горизонтальной  и вертикальной осей симметрии двух тел. Данная точка будет  являться центром   всех  проводимых из нее окружностей (концентрических сфер).

4.  Определяем максимальный радиус сферы. Он равен расстоянию от точки  О  до точки 2 – самой удаленной точки от центра. Все строящиеся в дальнейшем окружности должны быть меньшего диаметра.

5.  Определяем минимальный радиус сферы. Он равен величине перпендикуляра, проведенного из центра О до очерка наибольшего геометрического тела - усеченного конуса. Вписываем минимальную сферу в конус и определяем самую глубокую точку, принадлежащую линии пересечения.

6.  Вписанная сфера соприкасается с  конусом в двух точках и пересекает очерк другого геометрического тела  в двух местах.  Соединяем  найденные точки  прямыми линиями. Пересечение горизонтального и вертикального отрезков позволят определить самую глубокую точку, принадлежащую линии пересечения поверхностей.   

7.  Величина радиусов промежуточных окружностей, проводимых  из центра О должна быть не больше максимального и не меньше минимального радиусов.  Дальнейшие действия по определению точек, принадлежащих линии пересечения поверхностей, сводятся к построению пересекающихся отрезков,  каждый из которых соединяет точки пересечения промежуточной сферы с очерками заданных геометрических тел.

 

                                                       1

                                                  

 

                                                     

 

                  2 

 

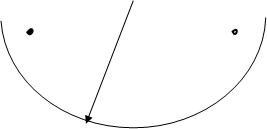
Рис. 91

8.  После того как определено достаточное для понимания формы линии пересечения количество точек, осуществляется соединение точек по лекалу. Вначале можно соединить точки от руки тонкой линией, а затем воспользоваться лекалом (рис. 91).

Итак,  использование данного способа для построения линии пересечения поверхностей возможно, если форма и расположение геометрических тел соответствуют  условиям  применения метода. Построение линии пересечения производится  в определенной последовательности (табл. 9).

Вопросы для самоконтроля

3.  Как  образуются многогранные поверхности?

4.  Как образуются поверхности вращения?

5.  Какие поверхности являются развертывающимися?

6.  Какие поверхности называются неразвертывающимися?

7.  Какими  способами можно построить проекции точек, находящихся на поверхностях?

8.  Как определяется форма  фигуры сечения многогранников  при рассечении  их плоскостями?

9.   Какие формы могут  принимать фигуры сечения   трехгранной пирамиды, рассеченной  различно расположенными секущими плоскостями?

10. Какие формы могут  принимать фигуры сечения шестигранной призмы, рассеченной   различно расположенными секущими плоскостями?

11. Какие формы могут  принимать фигуры сечения  цилиндра, рассеченного  различно расположенными секущими плоскостями?

12. Какие формы могут  принимать фигуры сечения  конуса, рассеченного  различно расположенными секущими плоскостями?

13. Какие формы могут  принимать фигуры сечения  сферы, рассеченной  различно расположенными секущими плоскостями?

14. В какой последовательности выполняется изображение фигуры сечения?

15. В какой последовательности выполняется построение точной развертки цилиндра, усеченного плоскостью?

16. В какой последовательности выполняется построение точной развертки конуса, усеченного плоскостью?

17. В какой последовательности выполняется построение точной развертки сферы, усеченной плоскостью?

18. Какие отличия существуют в построении приблизительных и точных   разверток тел вращения?

19. В чем сущность построения линии пересечения поверхностей способом вспомогательных секущих плоскостей?

20. В чем сущность построения линии пересечения поверхностей способом  концентрических сфер?

12. ОБЩИЕ СВЕДЕНИЯ О ЦЕНТРАЛЬНЫХ ПРОЕКЦИЯХ (перспективе).  ПРОЕЦИРУЮЩИЙ АППАРАТ И ЭЛЕМЕНТЫ КАРТИНЫ

Перспектива является центральной проекцией на картинную плоскость (плоскость проекций) и строится в соответствии с кажущимися изменениями величины формы объектов, наблюдаемыми в натуре. Перспективные изображения наглядны и соответствуют особенностям зрительного восприятия  человека. Перспективные (центральные) проекции широко используются  дизайнерами и архитекторами. Проекты зданий или интерьеров сопровождаются перспективным изображением проектируемого объекта.

Изображения в перспективе отличаются от аксонометрии. В  аксонометрических проекциях построение ведется по заданным осям и  параллельные  линии показываются параллельно (рис.91,а). В перспективных проекциях во многих случаях такие линии строятся сходящимися в точки схода на линии горизонта, а равные по величине отрезки прямых  уменьшаются по мере их удаления от точки зрения (рис. 91, б).  

 а                                                         б

Рис.91

В зависимости от вида проекционной поверхности перспектива подразделяется на несколько видов: линейную, плафонную, панорамную, купольную, театральную, наблюдательную.