VI)Позиционные задачи
20) Общие положения
20.1. Позиционные задачи – задачи, связанные с взаимным расположением фигур, включают задачи на взаимную принадлежность и на взаимное пересечение.
20.2. Прежде, чем рассматривать конкретные задачи, необходимо разобрать решение двух исходных задач: о принадлежности точки поверхности и о взаимном пересечении поверхностей, так как они используются для решения остальных позиционных задач.
Принадлежность точки поверхности
Для решения задачи о принадлежности точки поверхности необходимо:
§ вначале допустить, что точка принадлежит поверхности, то есть конкретной образующей поверхности
§ задать эту образующую, то есть на чертеже нанести ее проекции, при этом одну из этих проекций провести через проекцию точки, а вторую – исходя из условий принадлежности образующей поверхности
§ затем сравнить взаимное положение этой второй проекции образующей и заданной точки. Если эти проекции совпадают, то это значит, что точка принадлежит образующей, а следовательно и поверхности.
20.3. В общем случае можно взять и другую линию поверхности вместо образующей, но эта линия должна быть простой для построения на чертеже.
20.4. В итоге план решения задач на принадлежность точки поверхности включает:
§ определение вида заданной поверхности
§ выбор графической простой для построения на чертеже линии поверхности, проходящей через заданную точку
§ построение проекции этой линии на чертеже
§ построение искомых проекций точки
Взаимное пересечение поверхностей
 |
20.6. Для построения линии пересечения
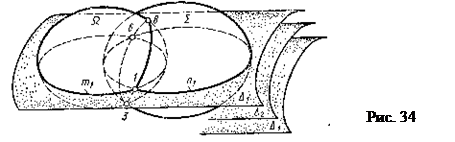
поверхностей необходимо использовать вспомогательные секущие поверхности ![]() … (рис. 34). При этом вначале находят линии пересечения m1, m2, n1, n2 … этих вспомогательных поверхностей с заданными
… (рис. 34). При этом вначале находят линии пересечения m1, m2, n1, n2 … этих вспомогательных поверхностей с заданными ![]() (омега)
и
(омега)
и ![]() (сигма). Затем для каждой
вспомогательной секущей поверхности в пересечении этих линий m1 и n1, m2 и n2, ... получают точки их пересечения — 1, 2, 3, ... Эти точки
принадлежат одновременно всем трем поверхностям — заданным и вспомогательной,
следовательно, и искомой линии пересечения. Число используемых вспомогательных
секущих поверхностей, следовательно, и построенных точек линии пересечения
зависит от требуемой точности решения задачи.
(сигма). Затем для каждой
вспомогательной секущей поверхности в пересечении этих линий m1 и n1, m2 и n2, ... получают точки их пересечения — 1, 2, 3, ... Эти точки
принадлежат одновременно всем трем поверхностям — заданным и вспомогательной,
следовательно, и искомой линии пересечения. Число используемых вспомогательных
секущих поверхностей, следовательно, и построенных точек линии пересечения
зависит от требуемой точности решения задачи.
Соединив на чертеже одноименные проекции найденных точек плавной линией, получаем проекции линии пересечения заданных поверхностей.
20.7. При построении линии пересечения поверхностей необходимо вначале найти опорные точки, а затем — промежуточные.
К опорным относят точки, лежащие на контурных линиях поверхности (т. е. отделяющие видимую часть линии пересечения от невидимой относительно соответствующей плоскости проекций); экстремальные точки (высшие, низшие и т. п.), а также точки, лежащие на ребрах и на линиях оснований поверхностей.
20.8. В качестве вспомогательных секущих поверхностей применяют плоскости и сферы. Для правильного выбора вспомогательной поверхности необходимо знать заданные поверхности.
20.9. В итоге план решения задач на взаимное пересечение поверхностей включает:
— определение вида заданных поверхностей;
— выбор вспомогательных секущих поверхностей;
— нахождение опорных точек линии пересечения;
— нахождение промежуточных точек линии пересечения;
— построение искомой линии пересечения с учетом ее видимости и формы, если она известна (прямая, окружность, эллипс).
21. Взаимная принадлежность геометрических фигур
21.1, Позиционные задачи на взаимную принадлежность геометрических фигур можно объединить в три группы.
Первая группа задач: принадлежность точки другой точке, а также прямой, плоскости и поверхности.
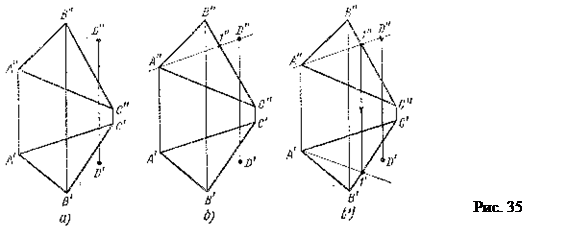
А. Принадлежность точки другой точке и прямой определяется по чертежу без дополнительных построений.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.