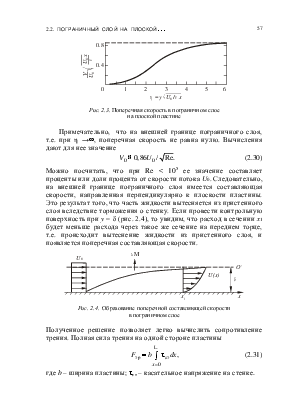







































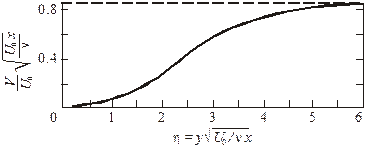
Рис. 2.3. Поперечная скорость в пограничном слое
на плоской пластине
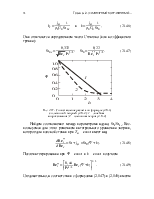
Примечательно, что на внешней границе пограничного слоя, т.е. при η →¥, поперечная скорость не равна нулю. Вычисления дают для нее значение
![]() (2.30)
(2.30)
Можно посчитать, что при Re < 105 ее значение составляет проценты или доли процента от скорости потока U0. Следовательно, на внешней границе пограничного слоя имеется составляющая скорости, направленная перпендикулярно к плоскости пластины. Это результат того, что часть жидкости вытесняется из пристенного слоя вследствие торможения о стенку. Если провести контрольную поверхность при у = δ (рис. 2.4), то увидим, что расход в сечении х1 будет меньше расхода через такое же сечение на переднем торце, т.е. происходит вытеснение жидкости из пристенного слоя, и появляется поперечная составляющая скорости.
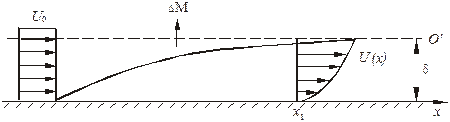
Рис. 2.4. Образование поперечной составляющей скорости
в пограничном слое
Полученное решение позволяет легко вычислить сопротивление трения. Полная сила трения на одной стороне пластины
![]() (2.31)
(2.31)
где b – ширина пластины; tст – касательное напряжение на стенке.
Обычно в расчетах принято использовать понятие коэффициента трения, представляющего собой безразмерное касательное напряжение
![]() ,
или
,
или ![]() (2.32)
(2.32)
Местное касательное напряжение на стенке
![]() , (2.33)
, (2.33)
или
![]() (2.34)
(2.34)
В соответствии с
результатами расчетов (см. табл. 2.1) ![]() тогда
коэффициент трения
тогда
коэффициент трения
![]() (2.35)
(2.35)
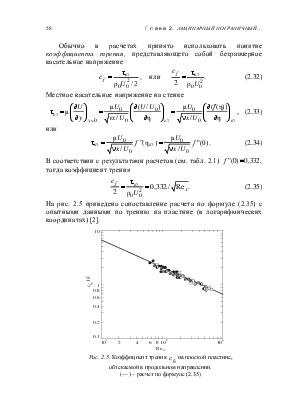
На рис. 2.5 приведено сопоставление расчета по формуле (2.35) с опытными данными по трению на пластине (в логарифмических координатах) [2].
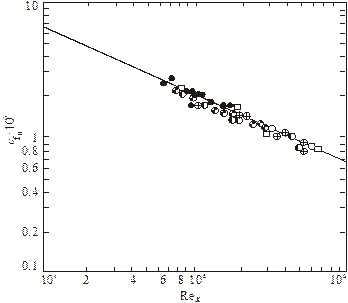
Рис. 2.5. Коэффициент трения ![]() на плоской
пластине,
на плоской
пластине,
обтекаемой в продольном направлении.
(—) – расчет по формуле (2.35)
Толщина
пограничного слоя не может быть определена точно, поскольку влияние стенки с
увеличением поперечной координаты уменьшается асимптотически, и значение
продольной составляющей скорости асимптотически переходит в скорость
потенциального течения. Если за толщину пограничного слоя принять расстояние от
стенки, на котором скорость U = 0,99U0, то из таблицы
найдем, что η » 5. Следовательно, толщина ламинарного пограничного слоя
![]() откуда
откуда ![]() , или
, или
![]() (2.36)
(2.36)
Можно рассчитать (зная U/U0) и другие интегральные характеристики пограничного слоя – толщину вытеснения и толщину потери импульса δ* и δ**. С этими понятиями мы познакомимся несколько позже.
2.3. Связь между трением, теплоотдачей
и диффузией. Тройная аналогия
При вынужденном конвективном движении существует примечательная связь между сопротивлением трения, теплоотдачей и диффузией в пограничном слое, на которую в ее простейшей форме указал еще Рейнольдс. Эту связь иногда называют «аналогией Рейнольдса» – аналогией между теплообменом и трением в пограничном слое.
Ниже мы рассмотрим этот вопрос в более общем виде применительно и к процессу массообмена, другими словами, тройную аналогию. Как было показано ранее (см., например, выражения (2.1) и (1.38)), уравнения движения, энергии и диффузии можно привести к безразмерной форме:
![]() (2.37)
(2.37)
![]() (2.38)
(2.38)
![]() (2.39)
(2.39)
Здесь ![]()
![]()
![]() –
безразмерные температура и концентрация;
–
безразмерные температура и концентрация; ![]()
Следует иметь в
виду, что уравнения энергии и диффузии в таком виде справедливы при ![]() т.е. Т и
С на стенке не зависят от продольной координаты, и поэтому они внесены
под знак дифференциала при приведении уравнений к безразмерному виду.
т.е. Т и
С на стенке не зависят от продольной координаты, и поэтому они внесены
под знак дифференциала при приведении уравнений к безразмерному виду.
Как видно, уравнения
движения, энергии и диффузии (2.37)…(2.39) становятся тождественными
при условии Pr = Sc = 1 и ![]() Cледовательно,
должны быть тождественны и их решения, т.е. подобны поля (безразмерные профили)
скоростей, температур и концентраций:
Cледовательно,
должны быть тождественны и их решения, т.е. подобны поля (безразмерные профили)
скоростей, температур и концентраций: ![]() ,или
,или
![]() (2.40)
(2.40)
Продифференцировав по у и положив у = 0, имеем
![]() (2.41)
(2.41)
Так как
![]() (2.42)
(2.42)
то из уравнения
(2.41) для рассматриваемых условий ![]() следует:
следует:
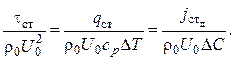 (2.43)
(2.43)
Здесь ![]() и поэтому в
(2.43) в двух последних членах изменился знак. (Размерность концентрации –
[кг/кг].)
и поэтому в
(2.43) в двух последних членах изменился знак. (Размерность концентрации –
[кг/кг].)
Первый член в этом
соотношении, мы уже знаем, представляет безразмерный коэффициент трения ![]() Второй член
принято называть числом Стентона (тепловым)*
Второй член
принято называть числом Стентона (тепловым)*
![]() (2.44)
(2.44)
где ![]() – коэффициент
теплоотдачи.
– коэффициент
теплоотдачи.
Последний член в уравнении (2.43) по аналогии с тепловым называют диффузионным членом Стентона
![]() (2.45)
(2.45)
Тогда окончательно в безразмерной форме связь между трением, теплоотдачей и диффузией имеет вид
![]() (2.46)
(2.46)
Полученное уравнение выражает гидродинамическую аналогию между трением, теплоотдачей и диффузией при Pr = Sc = 1.
Соотношение (2.46)
широко применяют в инженерных расчетах процессов тепломассообмена и трения.
Видно, что достаточно решить одну из задач, например динамическую, чтобы можно
было найти коэффициенты тепломассообмена. Иногда в практических расчетах
тепломассообмена используется не число Стентона, а число Нуссельта** ![]() (L – характерный
размер тела). Тогда имеем соотношение
(L – характерный
размер тела). Тогда имеем соотношение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.