Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 5

что практически совпадает с формулой (2.83). Газы имеют Pr < 1, для этого случая r > 1, и поэтому допущение, сделанное в приведенных расчетах (о том, что r < 1), строго говоря, не справедливо. Но так как минимальные значения для газов Pr ≈ 0,6, то r ≈ 1,16 и погрешность, обусловленная упомянутым допущением, очень мала.

Единственными веществами, которые характеризуются очень низкими значениями числа Прандтля (Pr < 10^-2), являются жидкие металлы. Для них формулы (2.83)…(2.86) непригодны.

Теплообмен при Pr << 1 (жидкие металлы)

При очень низких значениях Прандтля тепловой пограничный слой развивается значительно интенсивнее динамического (a >> n) и его толщина значительно больше толщины гидродинамического слоя, δ_т >> δ. Поэтому мы не допустим большой ошибки, если будем считать скорость по всей толщине теплового пограничного слоя постоянной и равной скорости внешнего потока, U_x = U₀.

Тогда выражение для толщины потери импульса можно представить в виде

.

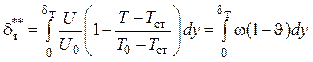С учетом выражения (2.68) для профиля температуры получим

                                         (2.87)

а для теплового потока на стенке –

                (2.88)

Подставляя (2.87) в (2.88), имеем

Приведя это выражение к безразмерному виду, получим закон теплообмена

.                         (2.89)

Решая интегральное уравнение энергии (2.65) совместно с законом теплообмена (2.89)

находим выражение для числа Рейнольдса, рассчитанного по толщине потери энергии

                                   (2.90)

Подставив это выражение в (2.89), получим распределение коэффициента теплообмена по длине пластины

                       (2.91)

Точное решение, приведенное в учебнике [2], дает

Тепловой ламинарный пограничный слой

при  U₀ = cx^m  и  ΔТ = ах^g

До сих пор мы изучали ламинарный пограничный слой при постоянной скорости на его внешней границе (U₀ = const) и при постоянной температуре стенки (T_ст = const), что справедливо только для обтекания пластины. Рассмотрим теперь более общий случай, когда эти величины могут изменяться по степенному закону. Для таких условий существуют точные автомодельные решения динамической и тепловой задач. Но, как было показано выше, более простым является интегральный метод решений, дающий в результате аналитические формулы, удобные для анализа. Поэтому интересно сопоставить результаты расчета теплообмена по приблизительному интегральному методу с точными автомодельными решениями.

Прежде чем анализировать эти решения, покажем, какие физические задачи характеризуются таким распределением скорости. Отметим, в частности, плоские потенциальные течения, характерные для обтекания клиновидных тел.

На рис. 2.7 показаны некоторые случаи плоских течений, удовлетворяющих зависимости U₀ = cx^m . При этом изменение скорости вдоль поверхности рассчитывается с помощью теории потенциальных течений

                                           (2.92)

где

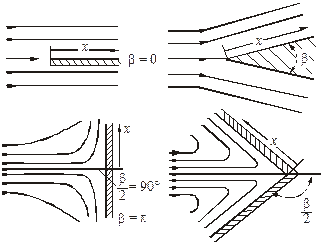
Рис. 2.7. Обтекание плоских и клиновидных тел

Частным их случаем является течение около плоской пластины при постоянной скорости внешнего потока (β = 0). К этому же семейству относится и плоское течение вблизи критической точки (β = π). Потоки со степенным изменением скорости на внешней границе пограничного слоя можно создать и в профилированном канале. Градиент давления на внешней границе пограничного слоя с учетом уравнения Бернулли представляет собой следующую функцию:

          (2.93)

Градиент давления прямо входит в дифференциальное уравнение движения пограничного слоя и может оказывать сильное влияние на профили скорости и сопротивление трения. В частности, при положительном градиенте давления (> 0 – замедленные течения) может наступить даже отрыв пограничного слоя. В точке отрыва пограничного слоя  а следовательно, равен нулю и коэффициент трения.