Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 6

На теплообмен же градиент давления влияет слабо. Это, в первую очередь, объясняется тем, что в дифференциальном уравнении энергии пограничного слоя отсутствует член, непосредственно связанный с градиентом давления. Его влияние в данном случае будет вторичным и выражается через деформацию профилей скоростей. Как показывают расчеты [1, 3], продольный градиент давления сравнительно слабо влияет на относительный закон теплообмена

                                (2.94)

и поэтому в инженерных расчетах им можно пренебречь:

                           (2.95)

В случае произвольного распределения скорости на внешней границе пограничного слоя значения коэффициента теплообмена могут быть приближенно определены с помощью интегрального метода.

Интегральные соотношения энергии пограничного слоя несжимаемой жидкости при обтекании непроницаемой поверхности:

– для плоского течения 

                (2.96)

– для осесимметричного течения 

        (2.97)

Решая задачи тепломассообмена интегральным методом, принимаем гипотезу о консервативности законов  и  в форме (2.95) при изменении граничных условий. Это означает, что используются законы для простейшего случая обтекания плоской пластины с постоянными температурой стенки (T_ст = const) и концентрацией диффундирующего компонента по длине пластины, и предполагается, что они слабо зависят от граничных условий и могут быть распространены на более сложные условия течения. К примеру, на течения с переменной скоростью на внешней границе пограничного слоя, переменной температурой или концентрацией на стенке. Тогда, принимая Ψ = 1 и подставляя (2.95) в уравнения (2.96) и (2.97), получаем линейные дифференциальные уравнения относительно :

для осесимметричного случая

Здесь в общем случае ΔТ, R_x, Re_L являются заданными функциями х. Интеграл  этого   дифференциального   уравнения   при граничных условиях х = 0,  имеет вид:

– для плоского течения

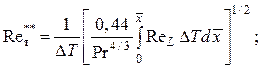                    (2.98)

– для осесимметричного случая

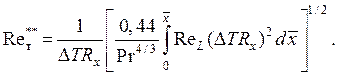                 (2.99)

Здесь следует иметь в виду, что число Рейнольдса Re_L = U₀L/n рассчитывается по локальной скорости на внешней границе слоя, зависящей от  х:  U₀ = cx^m, a ΔT = T_ст – T₀ = ax^γ (γ – параметр).

С учетом этих зависимостей из (2.99) получаем

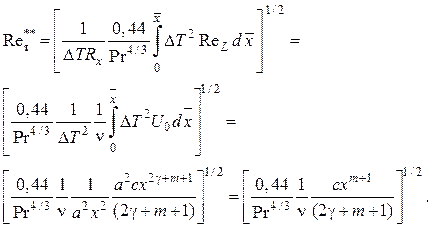
После подстановки

имеем соотношение для числа Рейнольдса

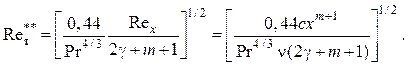       (2.100)

А выражение для числа Стентона при плоском сечении имеет вид

       (2.101)

и для числа Нуссельта –

        (2.102)

Для относительного коэффициента теплоотдачи при плоском течении получим простую формулу

                            (2.103)

где a₀ – значение коэффициента теплоотдачи в «стандартных» усло-виях (при постоянных температуре стенки и скорости основного по-тока, равной скорости в рассматриваемом сечении, т.е. γ = 0, m = 0)

                      (2.104)

а  Re_x = U₀x/n   определяется   по   локальной   скорости   основного потока (U₀ = cx^m).

Для  случая  обтекания   осесимметричного  тела при R_x = xⁿ, U₀ = cx^m, ΔT = ax^γ

                        (2.105)

и

                             (2.106)

Проанализируем изменение коэффициента теплообмена по длине в указанных условиях. Как следует из уравнений (2.103), (2.104) и (2.106),

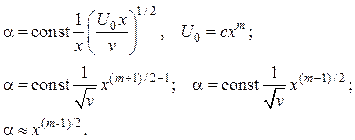          (2.107)

Заметим, что при m = 1 (β = π) в окрестности критической точки местный коэффициент теплоотдачи постоянен, a_х = const, т.е. пограничный слой имеет постоянную толщину. При m < 1 коэффициент теплоотдачи при х = 0 равен бесконечности и падает по длине пластины в направлении течения (в том числе и при m = 0 – обтекание плоской пластины). При  m > 1 a возрастает по х, начиная с нуля.

В учебнике [2] проведено сравнение приближенного метода расчета по формуле (2.102) с точным автомодельным методом решения  в  широкой области изменения параметров  m  и  γ (рис. 2.8).

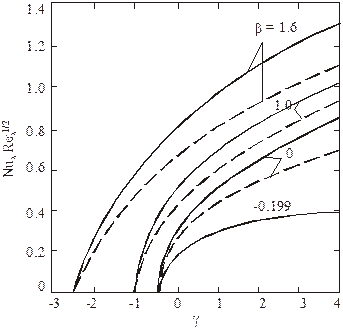
Рис. 2.8. Зависимость теплоотдачи от параметров β и γ

при Pr = 0,7: (–) – точное решение; (– – –) – расчет

по формуле (2.102)