Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 2

,   или                        (2.47)

–––––––––––––––––––––

*    По своему физическому смыслу число Стентона представляет собой отношение теплового потока в стенку к тому конвективному потоку, который может быть перенесен потоком жидкости при уменьшении ее температуры от T_ст  до  Т₀.

**  Число Нуссельта характеризует соотношение между конвективным переносом теплоты  от  жидкости  к  поверхности  тела  q_ст  и  переносом  теплоты  тепло-

      проводностью q_λ  через слой жидкости толщиной L.

Предыдущие рассуждения мы привели для ламинарного пограничного слоя. Однако существенно то, что аналогия Рейнольдса находит применение также и при турбулентном течении и играет важную роль при расчете процессов переноса.

В общем случае для Pr ≠ 1 можно получить формулу вида

                                        (2.48)

Функция f(Pr) при ламинарном течении приближенно равна , а при турбулентном f(Pr) = Pr^-0,6.

2.4.   Трение и теплообмен 

         при ламинарном течении на плоской  стенке.

         Метод Кармана – Польгаузена

2.4.1. Динамический пограничный слой

Интегральное соотношение импульсов, как мы уже установили, при безградиентном (dU₀/dx = 0) обтекании плоской стенки потоком газа с постоянными физическими свойствами имеет вид

                (2.49)

В этом уравнении одна независимая переменная х и две неизвестные функции . Для решения уравнения необходимо установить дополнительную связь между или, что то же самое, между c_f  и  Re^**. Зависимость c_f = f(Re^**) и будем называть законом трения.

Сущность приближенного метода Кармана – Польгаузена состоит в выборе подходящего выражения для профиля скоростей, которое должно удовлетворять физическим условиям задачи.  При этом используем свойство аффинности профилей скорости в пограничном слое, представив их в виде функции

В таком представлении функция f(η) не зависит от х. Результаты расчета будут тем точнее, чем ближе выбранные профили совпадут

с истинными. Выберем вид функции f(η) таким образом, чтобы удовлетворить граничным условиям:

при    у = 0:          U = 0;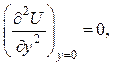    

при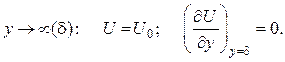

Условие того, что точка перегиба профиля скорости при безградиентном обтекании плоской непроницаемой поверхности лежит на стенке, следует из дифференциального уравнения движения при у → 0:

Производная  выражает собой условие плавности сопряжения профиля скорости с ее значением вне пограничного слоя (рис. 2.6). Будем искать функцию для профиля скорости f(η) в виде полинома третьей степени:

                          (2.50)

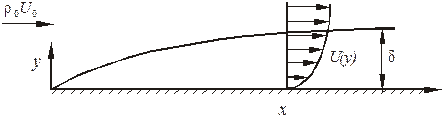
Рис. 2.6. Сопряжение профиля скорости пограничного слоя

с внешним течением

Коэффициенты в этой аппроксимации определяем с учетом граничных условий (2.49), записанных в безразмерном виде:

при   у = 0: 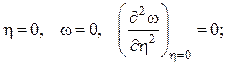                     (2.51)

при   у = δ: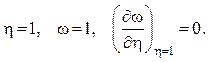                        

Используя эти условия из уравнения (2.50), имеем:

при  у = 0  η = 0,   ω = 0 = а,      а = 0;

при  η = 1  ω = 1 = а + b + c + d = 1;

при  η = 1 

b +2c + 3d = 0;

при  η = 0    c = 0.

Оставшиеся два неизвестных коэффициента определяются из со-отношений:

b + d = 1            b = 1 – d;

   b + 3d = 0           1 – d + 3d = 0 Þ d = –1/2, b = 3/2.

В результате получаем выражение для профиля скорости (2.50) в следующем виде:

                                     (2.52)

Имея профиль скорости, легко найти соотношения между интегральными характеристиками пограничного слоя:

                (2.53)

                      (2.54)

Из этих соотношений для толщины потери импульса и толщины вытеснения с учетом (2.52) получаем

           (2.55)

Интересно отметить, что точное решение Блазиуса для этих условий дает значение формпараметра Н = 2,59.

Определим теперь закон трения c_f = f(Re^**), который необходим для решения интегрального уравнения импульсов (1.78). Воспользуемся выражением касательного напряжения на стенке

                          (2.56)

Поскольку 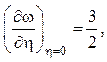 как следует из профиля скорости (2.52), учитывая   соотношения   (2.55)   для   толщины   потери   импульса, из (2.56) находим