Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 7

Отмечено удовлетворительное соответствие этих методов расчета (для самых крайних случаев расхождение не превышает 20 %). В частности, из уравнения (2.101) следует, что для плоского течения коэффициент теплоотдачи равен нулю при условии

                         (2.108)

что совпадает с точным решением.

На основании проведенного анализа можно прийти к выводу, что закон теплообмена, по крайней мере для степенного изменения скорости основного потока и температуры стенки, остается достаточно консервативным к изменению граничных условий. Это объясняется тем, что законы трения и теплообмена в такой форме были получены для локальных случаев, когда профили скорости и температуры удовлетворяли условиям на стенке и внешней границе слоя. А изменение граничных условий по длине поверхности учитывается при решении интегральный соотношений.

На этом основании рассмотренный метод расчета можно рекомендовать как первое приближение для произвольных граничных условий. Подставляя заданные законы изменения U₀ = f₁(x) и ΔТ  = = f₂(x) в уравнения (2.98), (2.99) и (2.95), получаем расчетные формулы для локальных значений числа Стентона.

Теплообмен при заданной тепловой нагрузке  q_ст = q_ст(x)

(граничные условия II рода)

В рассмотренных выше задачах мы задавались температурой стенки (граничные условия I рода) и при заданных гидродинамических условиях находили коэффициенты теплообмена. После этого не составляет труда определить тепловой поток, который необходимо снять (или подвести), чтобы обеспечить заданную температуру стенки:

Зависимость числа Стентона от числа Рейнольдса и других параметров течения при заданной температуре стенки была получена нами ранее.

Часто в инженерной практике встречаются задачи, когда при заданной тепловой нагрузке q_ст(х) требуется определить температуру стенки. Такие граничные условия называют граничными условиями II рода.

Уравнение энергии для непроницаемой стенки

можно переписать

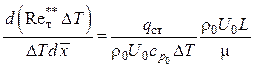, или

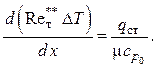
После интегрирования имеем

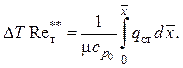                               (2.109)

Выразим число  через число St с помощью закона теплообмена:

     (2.110)

и подставим (2.110) в (2.109):

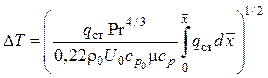, или с учетом того, что получим

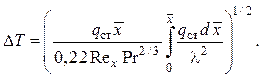                      (2.111)

Таким образом, при заданной тепловой нагрузке можно найти распределение температур по длине поверхности. Далее определяем и значение коэффициента теплоотдачи a_х = q_ст(x)/ΔT.

Для случая постоянной тепловой нагрузки (q_ст = const) коэф-фициент теплообмена определяется довольно просто. Интересно сравнить его со значением, полученным при граничных условиях I рода (T_ст= const). Как следует из уравнения (2.109), при q_cт = const справедливо равенство

 ,                                         (2.112)

или

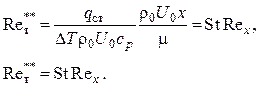                  (2.113)

Подставляя это значение в закон теплообмена, получаем

откуда имеем

                   (2.114)

или

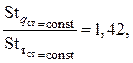                              (2.115)

т.е. коэффициент теплообмена при постоянном тепловом потоке выше примерно в полтора раза, чем при Т_ст = const (для одинаковых гидродинамических условий).

Анализ точных решений для неизотермических условий [2, 3] течения ( = T_ст /T₀ ≠ 1), т.е. когда температурный фактор существенно отличен от единицы, показывает, что неизотермичность и сжимаемость газа (число Маха) относительно слабо влияют на законы трения и теплообмена в ламинарном пограничном слое. В этом случае влияние изменения физических свойств (вязкости, плотности и теплопроводности) может взаимно компенсироваться.

Поэтому решения, полученные для течения с постоянными физическими свойствами, сохраняют свою силу и для течений с переменными физическими свойствами в широком диапазоне изменения температурного фактора  = T_ст /T₀, и в инженерных расчетах влиянием неизотермичности при малых скоростях течения М < 1 обычно пренебрегают.

По рекомендациям многих исследователей, влияние неизотермичности и сжимаемости при сверхзвуковом течении газа можно учесть по формуле

         (2.116)