Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 3

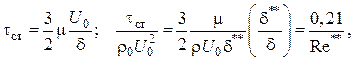
т.е. получаем закон трения для ламинарного пограничного слоя в «стандартных условиях»

                                    (2.57)

Интересно отметить, что из точного решения Блазиуса следует

                                          (2.58)

Подставляя (2.57) в (1.78), получаем

,                                 (2.59)

откуда

            (2.60)

Подставив это значение в закон трения, найдем изменение коэффициента трения по длине пластины

                                        (2.61)

Как мы помним, точное решение дифференциальных уравнений дает в этом выражении коэффициент 0,332.

Из выражения (2.60) имеем следующее соотношение для толщины потери импульса:

                                (2.62)

а с учетом (2.55)

                                        (2.63)

Пример.  Найдем   толщину   пограничного слоя на расстоянии 100 мм от переднего края пластины при движении воздуха вдоль ее поверхности. Скорость воздуха 10 м/с, температура – 20 °С и давление атмосферное. Значение   кинематической   вязкости  возьмем из  табл. 1.2, n»15×10^-6 м²/с. Число Рейнольдса, определяемое по текущей координате х,

тогда  откуда толщина пограничного слоя на расстоянии 100 мм от переднего края δ ≈ 1,8 мм.

Динамическая вязкость воды значительно больше, чем для воздуха (см. табл. 1.2),  Казалось бы, будет больше трение и толще пограничный слой. Но число Re_x обусловлено кинематической вязкостью Re_x = U₀x/n, а она для воды за счет высокой плотности ниже, чем для воздуха:  Поэтому при одинаковых значениях скорости течения число Рейнольдса для воды Re_х будет больше, а толщина пограничного слоя – меньше. Значение коэффициента трения будет также ниже для воды  а общее сопротивление трения выше,

Из приведенного примера видно, что при обычных условиях обтекания толщина пограничного слоя небольшая – порядка нескольких миллиметров. Поэтому к измерениям в пограничном слое, в частности к датчикам, предъявляются высокие требования.

2.4.2. Тепловой пограничный слой

Выше мы рассмотрели динамический пограничный слой и определили его характеристики – толщины δ, δ^*, δ^** и коэффициент трения. Используя аналогию Рейнольдса, мы можем теперь найти коэффициенты тепломассообмена

                                   (2.64)

Но эта тройная аналогия справедлива только при безградиентном  обтекании поверхности и при Т_ст = const. При этом тол-щины динамического, теплового и диффузионного слоев совпадают:

Ниже рассмотрим более общие случаи течения, когда Pr ≠ 1, Sc ≠ 1 и . Выкладки сделаем применительно к тепловому пограничному слою, но все эти результаты справедливы и для диффузионного слоя с заменой теплового числа Прандтля Pr на число Шмидта Sc, которое иногда называют диффузионным числом Прандтля.

Теплообмен на пластине

с начальным адиабатическим участком  d > d_T

Вернемся к рис. 1.1. Гидродинамический пограничный слой начинается у переднего края пластины, а тепловой несколько позже – у границы нагреваемой части. На начальном участке х₀ стенка имеет температуру T_ст = T₀, а при х > x₀ ее температура постоянна, T_ст = const и определяется условиями теплообмена. Необходимо рассчитать теплоотдачу в этих условиях. Для решения задачи используем интегральное соотношение энергии пограничного слоя, которое имеет вид

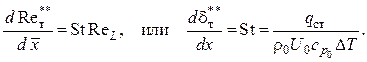        (2.65)

Профиль температуры аппроксимируем полиномом третьей степени

                   (2.66)

коэффициенты которого должны удовлетворять граничным условиям:

при у = 0: Т =Т_ст,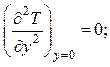

при 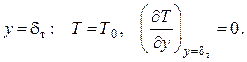                                        (2.67)

Условие  следует из дифференциального уравнения энергии, записанного для непроницаемой стенки, а  характеризует собой плавность сопряжения значений температуры на внешней границе пограничного слоя. В соответствии с этим определяем коэффициенты полинома (2.66) и получаем профиль температуры в виде

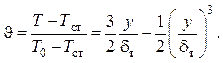                         (2.68)

Используя полученный ранее профиль скорости (2.52), можем найти толщину потери энергии

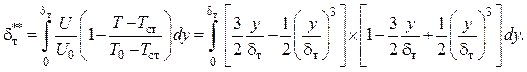
После интегрирования этого выражения, вводя обозначение r = δ_т/δ, получаем