Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 11

.                         (2.149)

Следовательно, в соответствии с формулами (2.147) и (2.149) имеем

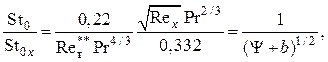            (2.150)

и так как

                                          (2.151)

то

                                     (2.152)

Тогда при Ψ  = 0, b = b_кр,  b_x = b_xкр

b_xкр = ( b_кр.)^1/2.                                  (2.153)

Отсюда видно, что выражение (2.145)

b_кр = 3,4/ε^2/3, соответствует полученному из точного решения при ε = 1 [см. (2.128)]

~1,86.

Порядок расчета тепломассообмена

на пористой поверхности

Интегральное соотношение энергии пограничного слоя на пористой поверхности в общем случае (T_ст = f(x), U₀ = f(x)) имеет вид

                (2.154)

Для ламинарного пограничного слоя закон теплообмена в стандартных условиях

                            (2.155)

Относительный закон теплообмена можно принять либо по пленочной теории (2.139), либо по более простой линейной зависимости (2.144):

                          (2.156)

Как видно из этих уравнений, для проведения расчета тепломассообмена необходимо предварительно найти значение параметра проницаемости b_Т. Он определяется в зависимости от граничных условий конкретной задачи. При пористом охлаждении охлаждающий газ подается через пористую стенку в пограничный слой.

Рассмотрим баланс теплоты на поверхности теплообмена при вдуве однородного газа (рис. 2.12). В стационарных условиях вся теплота, поступающая в пористую стенку, аккумулируется охлаждающим газом, а так как внутренняя поверхность пористого материала достаточно велика, можно полагать, что температура охлаждающего газа на выходе из пористой стенки равна температуре стенки. Тогда

                                 (2.157)

Приведя это уравнение к безразмерному виду, получим

где

                                       (2.158)

Если заданы температуры Т₀, T¢ и T_ст, то уравнение (2.158) по существу определяет параметр проницаемости b_T1 в случае пористого охлаждения.

Так как

b_T = b_T1Ψ = Ψ/K,         (2.159)

то, подставляя сюда значение Ψ из (2.156), получаем

        (2.160)

Обычно при расчетах пористого охлаждения требуется найти расход вдуваемого газа, необходимого для обеспечения заданной температуры поверхности тела. При известном законе изменения температур стенки и вдуваемого газа из уравнения (2.160) получают локальные значения параметра проницаемости b_Т.

В  частности, условие T_ст = const соответствует условию b_T = const (K = const; b = const; Ψ = const). С учетом выражения для b_T, см. (2.142),  имеем

                                    (2.161)

Значение числа Стентона St₀  определяется из решения интегрального соотношения энергии (2.154) совместно с (2.155).

В общем виде имеем

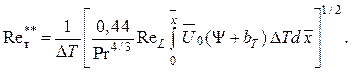          (2.162)

Здесь 

Для случая T_ст = const, T¢= const (K = const; b = const; Ψ = const) и U₀ = const, что может быть, например, на плоской стенке, выражение (2.162) упрощается:

                        (2.163)

Тогда расчетная формула для расхода охлаждающего газа (2.161) с учетом (2.155) и (2.163) примет вид

                         (2.164)

где b определится по (2.160), а Ψ – по (2.156). Или с учетом того, что b_T = b_T1Ψ,  выражение (2.164) можно записать иначе:

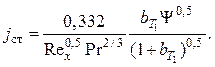                           (2.165)

В этом случае значение параметра b_T1 определяется в соответствии (2.158), b_T1 = 1/К, а относительная функция Ψ находится из уравнения (2.142) пленочной теории

Таким образом, для поддержания постоянной температуры стенки расход вдуваемого газа должен изменяться по закону j_ст ~ x^-0,5. Если проделать эти же выкладки  для   степенного закона   изменения   скорости основного потока  то получим, что в окрестности лобовой точки (когда m = 1) j_ст = const.

В случае, например, испарения или сублимации с поверхности определению подлежит количество отводимого от поверхности пара. Расход пара находим из уравнения теплового баланса на поверхности

где r – скрытая теплота фазового перехода (испарения).

После нескольких преобразований получим b_т = Ψ/К, К = r/c_pΔT – критерий Кутателадзе (критерий фазового перехода). Далее расчет можно вести по тем же формулам, что и для пористой стенки.