Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 4

                            (2.69)

Так как в нашем случае δ_т < δ, следовательно, r < 1, то второй член в правой части равенства будет весьма мал по сравнению с первым и им можно пренебречь:

                                    (2.70)

Запишем выражения для напряжения трения на стенке и для теплового потока с учетом профиля скорости (2.52) и профиля температуры (2.68):

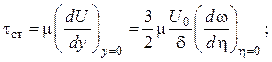                   (2.71)

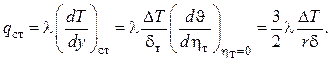             (2.72)

Подставим эти выражения в интегральные уравнения импульсов и энергии:

                (2.73)

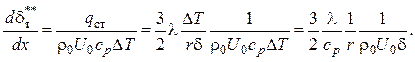    (2.74)

Используя полученное ранее соотношение для толщины потери импульса, уравнение (2.73) можно привести к виду

         (2.75)

Выражение же для толщины потери энергии (2.73) подставим в (2.74):

Продифференцируем левую часть:

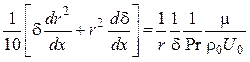
и перенесем r и δ из правой части в левую:

С учетом того, что  имеем

                         (2.76)

Подстановка  из уравнения (2.75) и значения δ² из (2.63)

в уравнение (2.76) дает:

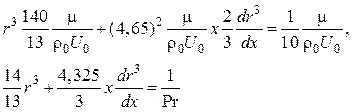          (2.77)

или

.

Делая подстановку r³ = у, получаем

или

                           (2.78)

– линейное неоднородное дифференциальное уравнение*.

______________________

* Для решения линейного неоднородного дифференциального уравнения используется метод Лагранжа – метод вариации постоянной. Запишем уравнение (2.78) в общем виде:

.                                                        (1)

Сначала решается однородное уравнение:  В нашем случае оно имеет вид, см. (2.78)

,   или  

Проинтегрировав его, получим

или

                                         (2)

Далее принимается, что постоянная с₁ есть неизвестная функция от х, которую нужно определить,

с₁ = φ(х).                                                            (3)

Тогда

                                                    (4)

Продифференцируем (4) по х:

                     (5)

Подставляя (4) и (5) в уравнение (2.78), находим значение, которое удовлетворяет этому уравнению:

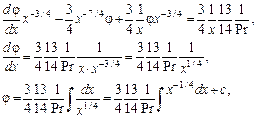
Затем  подставляем φ(х) в уравнение (4) и определяем у.

Решение уравнения (2.78) имеет вид

              (2.79)

Из граничных условий для х = х₀, r = δ_т / δ = 0 следует

Подставляя последнее в (2.79), имеем

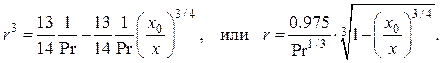     (2.80)

Тепловой поток в соответствии с формулой (2.72) можно определить так:

                       (2.81)

т.е. коэффициент теплообмена обратно пропорционален толщине теплового пограничного слоя.

Подставляя в выражение для коэффициента теплообмена значения r (2.80) и толщины динамического пограничного слоя  получаем

или, переходя к числу Стентона,

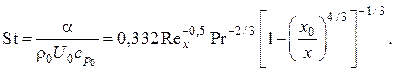      (2.82)

Для плоской  стенки, нагреваемой по всей длине х₀ → 0,

                            (2.83)

По уравнению (2.83) можно вычислить распределение плотности теплового потока по длине пластины. Однако чаще интересуются полным тепловым потоком, передаваемым от пластины конечной толщины. Из приведенного решения (2.83) следует, что

Для определения полного теплового потока необходимо вычислить средний по х коэффициент теплоотдачи:

Тогда уравнение для среднего числа Стентона имеет вид

Решая совместно с этим выражением интегральное соотношение энергии

, получим соотношение между числами Рейнольдса, построенными по толщине потери энергии  и длине пластины х,

                         (2.84)

Подставив это соотношение в (2.83), найдем закон теплообмена для стандартных условий

                                      (2.85)

Если пластина нагревается по всей длине (х₀ = 0), то соотношение между толщинами теплового и динамического слоев будет постоянно и определится только значением числа Pr:

                            (2.86)

Вязкие масла имеют критерий Прандтля Pr ≈ 1000 и больше. Для этих жидкостей толщина теплового пограничного слоя составляет только примерно  1/10  толщины   гидродинамического погранично-го слоя, т.е. при n > a возмущения, обусловленные молекулярным трением, распространяются на большую область, чем возмущения, обусловленные молекулярной теплопроводностью.

При Pr → ∞ точное  решение, полученное в работах [1, 2], дает