Связь между трением, теплоотдачей и диффузией. Тройная аналогия, страница 10

– при   у = δ:    U = U₀,   T = T₀.                                              (2.132)

Поскольку из (2.129), следует, что ρV = const = j_ст, решения уравнений (2.130) и (2.131) с учетом граничных условий (2.132) дают профили скорости и температуры в следующем виде*:

             (2.133)

.     (2.134)

___________________________

* Вывод уравнения (2.133) предлагается сделать самостоятельно.

Здесь  Касательное напряжение на стенке τ_ст может быть определено так:

Из (2.133) следует, что

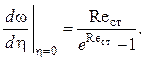
Тогда

                       (2.135)

С другой стороны, исходя из пленочной модели течения при отсутствии вдува, можно получить

                                    (2.136)

Таким образом, при одинаковых значениях δ или Re_δ = ρ₀U₀δ/μ из уравнений (2.135) и (2.136) получаем относительный закон трения

                 (2.137)

где

С учетом (2.136)

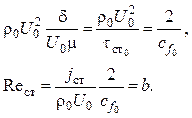                             (2.138)

Здесь b – параметр проницаемости, рассчитанный по коэффициенту трения в стандартных условиях c_f0.

С учетом этого относительный закон трения (2.138) можно переписать:

                        (2.139)

Иногда используют параметр проницаемости, рассчитанный по коэффициенту трения на проницаемой пластине (в рассматриваемых условиях):

                         (2.140)

В этом случае выражение (2.139) преобразуется к виду

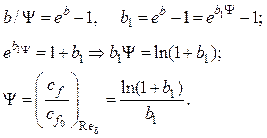                  (2.141)

В первом приближении можно принять, что

.

Проведя аналогичное решение уравнения энергии на проницаемой и непроницаемой стенках, получим, что

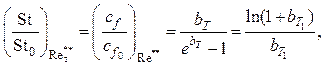            (2.142)

где 

Пленочная теория дает приемлемые результаты при малых и умеренных вдувах. При интенсивных вдувах, как было показано выше, точное автомодельное решение ламинарного пограничного слоя, учитывающее в уравнениях движения и энергии продольные градиенты  предсказывает полное оттеснение пограничного слоя от стенки (при b_x = 1,86, Ψ = 0).

Пленочная теория, см. уравнения (2.140) и (2.142), дает асимптотическое уменьшение коэффициентов трения и теплообмена до нуля при b→ ∞. Здесь следует отметить, что пленочная теория используется для анализа влияния вдува как в ламинарном, так и в турбулентном пограничном слое [3]. Исследователями показано, что полученные зависимости хорошо  описывают уменьшение пере-носа теплоты при вдуве в ламинарном пограничном слое при Pr ~ 1.

Некоторые аппроксимации точных решений

В известных научных статьях и монографиях, например в работе [3], обобщаются результаты численных решений уравнений ламинарного пограничного слоя на проницаемой пластине и предлагается следующая формула для расчета локального теплообмена:

                       (2.143)

Здесь ε = М₀ /M¢ – отношение молекулярной массы основного потока и вдуваемого  газа;   q_ст0  – тепловой   поток на непроницаемой пластине при  Re_x = idem и том же значении ΔТ.

Физические параметры, входящие в Re_x, рассчитываются при определяющей температуре

Эта формула справедлива как для дозвукового, так и для сверхзвукового обтекания. Однако, как указано в работе [5] С.С. Кутателадзе, она дает удовлетворительные результаты при умеренных вдувах, b/b_кр < 0,6.

Наиболее простая линейная аппроксимация с достаточной степенью точности предложена А.И. Леонтьевым [2]:

                (2.144)

где

                         (2.145)

Как видно из графиков (рис. 2.11), для практических расчетов ламинарного пограничного слоя со вдувом можно использовать линейную аппроксимацию (2.144).

При анализе пограничного слоя на проницаемой стенке применяют два вида параметра вдува

                    (2.146)

Они отличаются определением чисел Стентона (или коэффициента трения):

                (2.147)

Ψ

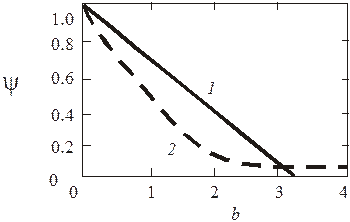
Рис. 2.11.  Сопоставление расчета по формуле (2.144)

с пленочной  теорией (2.142): 1 – линейная

аппроксимация; 2 – пленочная теория (2.142)

Найдем соотношение между параметрами вдува, St₀/St_0x. Вос-пользуемся для этого решением интегрального уравнения энергии, которое для плоской стенки при T_cт = const имеет вид

                      (2.148)

После интегрирования при  Ψ = const  и  b = const  получаем